
分析 (1)利用放缩法和绝对值三角不等式的性质即可证明,
(2)由已知a+b+c=3,利用基本不等式即可证明
解答 证明:(1)$|f(a)-f(b)|=|\sqrt{1+{a^2}}-\sqrt{1+{b^2}}|=\frac{{|1+{a^2}-1-{b^2}|}}{{\sqrt{1+{a^2}}+\sqrt{1+{b^2}}}}$$<\frac{{|{a^2}-{b^2}|}}{{\sqrt{a^2}+\sqrt{b^2}}}=\frac{|a-b||a+b|}{|a|+|b|}≤\frac{|a-b||a+b|}{|a+b|}=|a-b|$
若a+b=0时,不等式显然成立.
(2)由已知a+b+c=3,
则3(a+b+c)=(a+b+c)2=a2+b2+c2+2ab+2bc+2ca,
=$\frac{1}{2}({a^2}+{b^2})+\frac{1}{2}({b^2}+{c^2})+\frac{1}{2}({c^2}+{a^2})+2ab+2bc+2ca$,
≥ab+bc+ca+2ab+2bc+2ca,
=3(ab+bc+ca)
故a+b+c≥ab+bc+ca.
点评 本题考查了绝对值的三角不等式和基本不等式的应用,考查了学生的转化能力,属于中档题


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:解答题
| 物理及格 | 物理不及格 | 合计 | |
| 数学及格 | 28 | 8 | 36 |
| 数学不及格 | 16 | 20 | 36 |
| 合计 | 44 | 28 | 72 |
| P(X2≥k) | 0.150 | 0.100 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
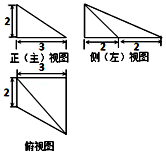
| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | $\sqrt{29}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | $(-\frac{12}{5},-\frac{12}{5})$ | C. | (-3,0) | D. | $(\frac{12}{5},\frac{12}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
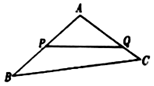 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com