Question

10．在平面内，$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\overrightarrow{CA}$•$\overrightarrow{CB}$=6，若动点P，M满足|$\overrightarrow{AP}$|=2，$\overrightarrow{PM}$=$\overrightarrow{MC}$，则|$\overrightarrow{BM}$|的最小值是2．

Answer 1

分析 由$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\overrightarrow{CA}$•$\overrightarrow{CB}$=6，可知△ABC是边长为2$\sqrt{3}$的等边三角形，P在以A为圆心的圆上，建立坐标系，设出P点坐标，求出$\overrightarrow{BM}$的坐标，根据模长公式即可得出|$\overrightarrow{BM}$|²关于θ的函数，利用三角恒等变换求出此函数的最大值即可

解答 解：∵$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\overrightarrow{CA}$•$\overrightarrow{CB}$=6，∴$\overrightarrow{AB}•（\overrightarrow{AC}+\overrightarrow{BC}）$=0，$\overrightarrow{BC}•（\overrightarrow{BA}+\overrightarrow{CA}）$=0，$\overrightarrow{AC}•（\overrightarrow{AB}+\overrightarrow{CB}）$=0，
∴△ABC是等边三角形，设△ABC的边长为a，
∴$\overrightarrow{AB}•\overrightarrow{AC}$=a²cos60°=$\frac{1}{2}$=6，∴a=2$\sqrt{3}$．
∵|$\overrightarrow{AP}$|=2，∴P在以A为圆心，以2为半径的圆上，
∵$\overrightarrow{PM}$=$\overrightarrow{MC}$，∴M是PC的中点，
以BC为x轴，以BC的中垂线为y轴建立坐标系，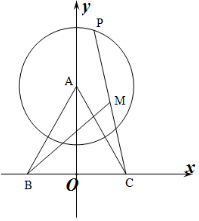
则B（-$\sqrt{3}$，0），C（$\sqrt{3}$，0），A（0，3），
设P（2cosθ，3+2sinθ），则M（cosθ+$\frac{\sqrt{3}}{2}$，$\frac{3}{2}$+sinθ），
∴$\overrightarrow{BM}$=（$\frac{3\sqrt{3}}{2}$+cosθ，$\frac{3}{2}$+sinθ），
∴|$\overrightarrow{BM}$|²=（$\frac{3\sqrt{3}}{2}$+cosθ）²+（$\frac{3}{2}$+sinθ）²=3$\sqrt{3}$cosθ+3sinθ+10=6sin（θ+$\frac{π}{3}$）+10，
∴当sin（θ+$\frac{π}{3}$）=-1时，|$\overrightarrow{BM}$|²取得最小值4．
|$\overrightarrow{BM}$|的最小值是2；
故答案为：2．

点评 本题考查了平面向量的数量积运算，坐标法可使计算简化，属于中档题．