
分析 (I)设等差数列{an}的公差为d,由题意,得$\left\{\begin{array}{l}10{a_1}+45d=3({5{a_1}+10d})+20\\{a_1}+({2n-1})d=2[{{a_1}+({n-1})d}]\end{array}\right.$,解得解得a1=2,d=2,用等差数列的通项公式即可得出.
(II)bn=$\frac{2n+1}{4(n+1)^{2}-4{n}^{2}}$=$\frac{1}{16}$[$\frac{1}{{n}^{2}}$-$\frac{1}{(n+1)^{2}}$],利用“裂项求和”、“放缩法”即可得出.
解答 解:(Ⅰ):设等差数列{an}的公差为d,由题意,得$\left\{\begin{array}{l}10{a_1}+45d=3({5{a_1}+10d})+20\\{a_1}+({2n-1})d=2[{{a_1}+({n-1})d}]\end{array}\right.$,
解得a1=2,d=2,
∴an=2n,n∈N*,
(Ⅱ)∵an=2n,n∈N*,
∴bn=$\frac{2n+1}{4(n+1)^{2}-4{n}^{2}}$=$\frac{1}{16}$[$\frac{1}{{n}^{2}}$-$\frac{1}{(n+1)^{2}}$],
则${T_n}=\frac{1}{16}[{1-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{3^2}-\frac{1}{4^2}+…+\frac{1}{n^2}-\frac{1}{{{{({n+1})}^2}}}}]$=$\frac{1}{16}[{1-\frac{1}{{{{({n+1})}^2}}}}]$,
∵n∈N*,
∴$\frac{3}{64}≤{T_n}<\frac{1}{16}$.
点评 本题考查了“裂项求和”、等差数列的通项公式、递推式的应用、“放缩法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 虚数集和各个象限内的点的集合是一一对应的 | |
| B. | 实、虚部都是负数的虚数的集合与第二象限的点的集合是一一对应的 | |
| C. | 实部是负数的复数的集合与第二、三象限的点的集合是一一对应的 | |
| D. | 实轴上侧的点的集合与虚部为正数的复数的集合是一一对应的 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x>1,则x2>1”的逆命题 | B. | 命题“若x=1,则x2+x-2=0”的否命题 | ||
| C. | 命题“若x>y,则x>|y|”的逆命题 | D. | 命题“若x2>0,则x>-1”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}∈M$ | B. | 1∉M | C. | M是空集 | D. | 该集合是有限集 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{14}{9}$ | C. | $\frac{9}{14}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过圆内接四边形ABCD的顶点C引切线MN,AB为圆的直径.
如图,过圆内接四边形ABCD的顶点C引切线MN,AB为圆的直径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
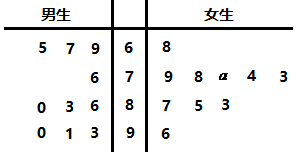 某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).
某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com