
| 4 |
| 7 |
| 1 |
| 22 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| n |
| 7 |
| x |
| 7 |
| 2x |
| 7 |
| 2x |
| 7 |
| 2x |
| 5 |
| 2 |
| 4 |
| 7 |
| 2x2+2ax-4a2 |
| x |
| 2(x-a)(x+2a) |
| x |
| 5 |
| 2 |
| 5 |
| 2 |
| n+1 |
| n |
| 7 |
| x |
| 7 |
| x |
| 7 |
| 2x |
| 7 |
| 2x |
| 7 |
| 2x |
| 5 |
| 2 |
| 5 |
| 2 |
| 4 |
| 7 |
| 2x2+2ax-4a2 |
| x |
| 2(x-a)(x+2a) |
| x |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 53 |
| 4 |
| n+1 |
| n |
| 1 |
| n |
| 1 |
| n |
| n+1 |
| n |
| 1 |
| n2 |
| 1 |
| n |
| 1 |
| 12 |
| 7 |
| 1 |
| 1 |
| 22 |
| 7 |
| 2 |
| 1 |
| n2 |
| 7 |
| n |
| 1 |
| 22 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| n |


科目:高中数学 来源: 题型:
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| 得分 | 25 | 35 | 21 | 33 | 25 | 16 | 34 | 18 |
| 编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| 得分 | 17 | 38 | 15 | 28 | 22 | 12 | 31 | 26 |
| 区间 | [10,20] | [20,30] | [30,40] |
| 人数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
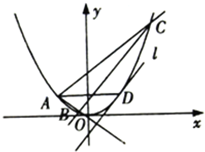 已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行
已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax |
| x+1 |
| f(x1)+f(x2) |
| x+1 |
| f(x)+2 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
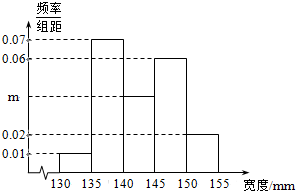 1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.
1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.| m | 中位数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
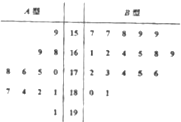 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com