
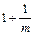 <a1<
<a1<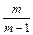 (m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。
(m为常数且m∈N+,m≠1),求最小自然数N,使得当n≥N时,总有0<an<1成立。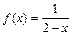
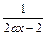 ,
,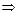
 , ∴
, ∴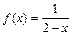 , 4 分
, 4 分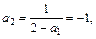
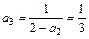 ,
,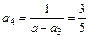 ,
,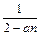 <
<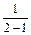 =1
=1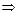 2-an>0,从而an+1-an=
2-an>0,从而an+1-an=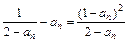 >0
>0 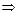 an+1>an 从第2项起,数列{an}中的项满足an<an+1 9分
an+1>an 从第2项起,数列{an}中的项满足an<an+1 9分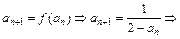
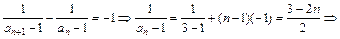
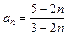
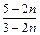 <
<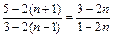 ,
, 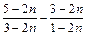 <0
<0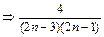 >0
>0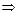 n>
n>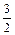 或n<
或n<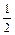 ,又∵n∈N*,∴n>
,又∵n∈N*,∴n>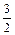 ,∴从第2项起,数列{an}中的项满足an<an+1 9分
,∴从第2项起,数列{an}中的项满足an<an+1 9分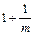 <a1<
<a1<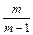 时,由
时,由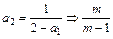 <a2<
<a2<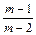 ,同理
,同理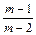 <a3<
<a3<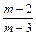 ,假设
,假设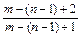 <an<
<an<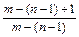 ,由
,由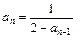 与归纳假设知
与归纳假设知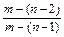 <am,即am>2
<am,即am>2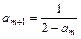 <0,0<am+2=
<0,0<am+2=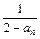 <
<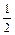 ="1 " ∴N=m+2,使得当n≥N时,总有0<an<1 14分
="1 " ∴N=m+2,使得当n≥N时,总有0<an<1 14分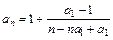
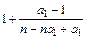 <1
<1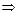 -1<
-1<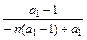 <1
<1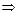 -1<
-1<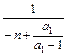 <0
<0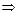
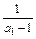 <n-2时,总有0<an<1,又∵
<n-2时,总有0<an<1,又∵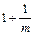 <a1<
<a1<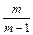 <m-1<
<m-1<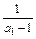 <m
<m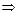 n≥m+2 ∴当N=m+2,使得当n≥N时总有0<an<1 14分
n≥m+2 ∴当N=m+2,使得当n≥N时总有0<an<1 14分

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com