
| A. | -20 | B. | 20 | C. | -70 | D. | 70 |
分析 根据分段函数求出f[f(x)]的解析式,再利用二项式展开式的通项公式即可求出展开式的常数项.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{(x-\frac{1}{x})^{8},x<0}\\{-\sqrt{x},x≥0}\\{\;}\end{array}\right.$,
∴当x>0时,f[f(x)]=f(-$\sqrt{x}$)=${(-\sqrt{x}+\frac{1}{\sqrt{x}})}^{8}$=${(\sqrt{x}-\frac{1}{\sqrt{x}})}^{8}$,
其展开式的通项公式为
Tr+1=${C}_{8}^{r}$•${(\sqrt{x})}^{8-r}$•${(-\frac{1}{\sqrt{x}})}^{r}$=(-1)r•${C}_{8}^{r}$•x4-r,
令4-r=0,解得r=4;
∴展开式的常数项为:
T5=(-1)4•${C}_{8}^{4}$=70.
故选:D.
点评 本题考查了分段函数与二项式展开式通项公式的应用问题,是基础题目.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 样本方差反映了所有样本数据与样本平均值的偏离程度 | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好 | |
| D. | 在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是残差平方和 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
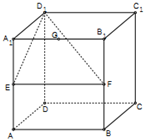 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com