
| A. | f(x2)<f(x-1) | B. | (x-1)f(x)<xf(x+1) | C. | f(x)>x-1 | D. | f(x)<0 |
分析 造函数g(x)=(x-1)f(x),得到g(x)在R上单调递减,根据g(1)=0,得到x>1时:f(x)<0,从而求出答案.
解答 解:∵f(x)定义在R上的增函数,其导函数为f′(x),
∴f′(x)>0,
∵(x-1)f′(x)+f(x)<0,
设g(x)=(x-1)f(x),
∴g′(x)=(x-1)f′(x)+f(x)<0,
∴g(x)在R上单调递减,
∵g(1)=0,、
∴当x>1时:g(x)=(x-1)f(x)<g(1)=0,
∴x>1时:f(x)<0,
又f(x)是定义在R上的增函数,
∴当x≤1时:必有f(x)<0,
综上可知f(x)<0,x∈R,
故选:D.
点评 本题考查了导数的应用,考查函数的单调性问题,构造函数g(x)=(x-1)f(x),根据x>1时得到f(x)<0是解题的关键,本题是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
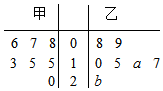 甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲乙两家快餐店对某日7个时段来店光临的客人人数进行统计绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=1,AB=AC=$\sqrt{2}$,D为BC的中点,过点D作DQ平行于AP,且DQ=1.连接QB,QC,QP
如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=1,AB=AC=$\sqrt{2}$,D为BC的中点,过点D作DQ平行于AP,且DQ=1.连接QB,QC,QP查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com