
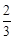 ……………………5分
……………………5分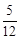 ,小华获胜的概率为
,小华获胜的概率为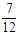 … … ……11分
… … ……11分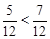 ,所以这个游戏不公平. … … ……12分
,所以这个游戏不公平. … … ……12分

 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:不详 题型:解答题
| 排队人数 |  |  |  |  |  |  人以上 人以上 |
| 概率 |  |  |  |  |  |  |
 人排队的概率是多少?
人排队的概率是多少?  人排队的概率是多少
人排队的概率是多少查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的高二(1)班男同学有
的高二(1)班男同学有 名,女同学有
名,女同学有 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;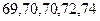 ,第二次做试验的乙同学得
,第二次做试验的乙同学得 到的试验数据为
到的试验数据为 ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. .
. 的回归直线方程是:
的回归直线方程是: ,使代数式
,使代数式



 的值最小时,
的值最小时, ,
, ,(
,( 、
、 分别是这三组数据的横、纵坐标的平均数)
分别是这三组数据的横、纵坐标的平均数)| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
 ,即称
,即称 为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.
为(Ⅰ)中回归直线的拟和“好点”,求后四组数据中拟和“好点”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 10 | 15 | 20 | 25 | 30 |
| y | 1003 | 1005 | 1010 | 1011 | 1014 |
 B.
B.
 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com