
分析 求出$\overrightarrow{a}+\overrightarrow{b}$的坐标,根据|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$列出方程解出sin2x,再根据x的范围解出x.
解答 解:$\overrightarrow{a}+\overrightarrow{b}$=(cos$\frac{3}{2}x$-sin$\frac{x}{2}$,sin$\frac{3}{2}x$-cos$\frac{x}{2}$).
∴|$\overrightarrow{a}+\overrightarrow{b}$|2=(cos$\frac{3}{2}x$-sin$\frac{x}{2}$)2+(sin$\frac{3}{2}x$-cos$\frac{x}{2}$)2=2-2cos$\frac{3}{2}x$sin$\frac{x}{2}$-2sin$\frac{3}{2}x$cos$\frac{x}{2}$=2-2sin2x.
∵|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,
∴2-2sin2x=3,∴2sin2x=-1,sin2x=-$\frac{1}{2}$.
∵x∈[$\frac{π}{2}$,π],∴2x∈[π,2π].
∴2x=$\frac{7π}{6}$或2x=$\frac{11π}{6}$.
∴x=$\frac{7π}{12}$或x=$\frac{11π}{12}$.
点评 本题考查了平面向量的坐标运算,模长计算,三角函数的恒等变换,属于中档题.


科目:高中数学 来源: 题型:解答题
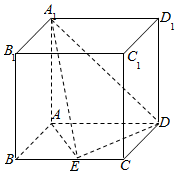 如图,在长方体ABCD-A1B1C1D1中,AA1=$\sqrt{2}$,AB=1,AD=m(m>0),E为BC的中点,且∠A1ED=90°
如图,在长方体ABCD-A1B1C1D1中,AA1=$\sqrt{2}$,AB=1,AD=m(m>0),E为BC的中点,且∠A1ED=90°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com