
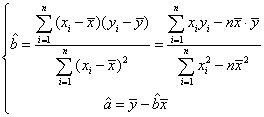 某中学有6名爱好篮球的高三男生,现在考察他们的投篮水平与打球年限的关系,每人罚篮10次,其打球年限与投中球数如下表:
某中学有6名爱好篮球的高三男生,现在考察他们的投篮水平与打球年限的关系,每人罚篮10次,其打球年限与投中球数如下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 打球年限 | 3 | 5 | 6 | 7 | 9 |
| 投中球数 | 2 | 3 | 3 | 4 | 5 |
(Ⅰ)求投中球数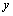 关于打球年限
关于打球年限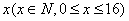 的线性回归方程,若第6名同学的打球年限为11年,试估计他的投中球数(精确到整数).
的线性回归方程,若第6名同学的打球年限为11年,试估计他的投中球数(精确到整数).
(Ⅱ)现在从高三年级大量男生中调查出打球年限超过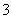 年的学生所占比例为
年的学生所占比例为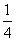 ,将上述的比例视为概率。现采用随机抽样方法在男生中每次抽取1名,抽取3次,记被抽取的3名男生中打球年限超过
,将上述的比例视为概率。现采用随机抽样方法在男生中每次抽取1名,抽取3次,记被抽取的3名男生中打球年限超过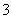 年的人数为X。若每次抽取的结果是相互独立的,求X的分布列,期望
年的人数为X。若每次抽取的结果是相互独立的,求X的分布列,期望 。
。
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
某国庆纪念品,每件成本为30元,每卖出一件产品需向税务部门上缴a元(a为常数,4≤a≤6)的税收.设每件产品的售价为x元,根据市场调查,当35≤x≤40时日销售量与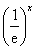 (e为自然对数的底数)成正比.当40≤x≤50时日销售量与
(e为自然对数的底数)成正比.当40≤x≤50时日销售量与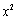 成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.
成反比,已知每件产品的售价为40元时,日销售量为10件.记该商品的日利润为L(x)元.
(1)求L(x)关于x的函数关系式;
(2)当每件产品的售价x为多少元时,才能使L(x)最大,并求出L(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四个命题中真命题的个数是 ( )
①若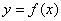 是奇函数,则
是奇函数,则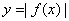 的图像关于
的图像关于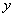 轴对称;②若
轴对称;②若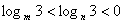 ,则
,则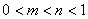 ;③若函数
;③若函数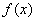 对任意
对任意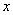 ∈R满足
∈R满足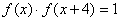 ,则8是函数
,则8是函数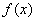 的一个周期;④命题“在斜
的一个周期;④命题“在斜 中,
中,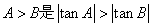 成立的充要条件;⑤命题
成立的充要条件;⑤命题
“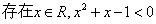 ”的否定是“
”的否定是“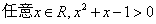 ”
”
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
已知极点为直角坐标系的原点,极轴为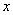 轴正半轴且单位长度相同的极坐标系中,
轴正半轴且单位长度相同的极坐标系中,
直线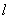 :
: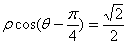 与直角坐标系中的曲线C:
与直角坐标系中的曲线C: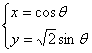 (
(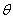 为参数),
为参数),
交于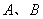 两点.
两点.
(Ⅰ)求直线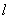 在直角坐标系下的方程;(Ⅱ)求点
在直角坐标系下的方程;(Ⅱ)求点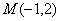 与
与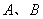 两点的距离之积
两点的距离之积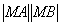 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系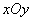 中,以坐标原点为极点,以
中,以坐标原点为极点,以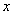 轴的非负半轴为极轴,建立极坐标系,已知直线
轴的非负半轴为极轴,建立极坐标系,已知直线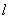 的参数方程为
的参数方程为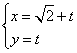 (t为参数),圆
(t为参数),圆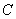 的极坐标方程是
的极坐标方程是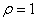 。
。
(I)求直线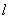 与圆
与圆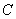 的公共点个数;
的公共点个数;
(II)在平面直角坐标系中,圆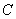 经过伸缩变换
经过伸缩变换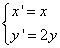 得到曲线
得到曲线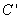 ,设
,设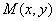 为曲线
为曲线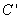 上一点,求
上一点,求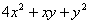 的最大值,并求相应点
的最大值,并求相应点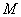 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com