
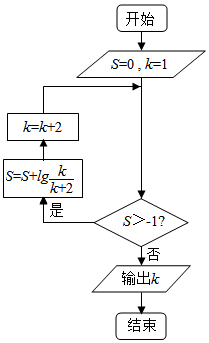
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量k的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:由题意,模拟执行程序框图,可得
S=0,k=1
满足条件S>-1,S=lg$\frac{1}{3}$,k=3
满足条件S>-1,S=lg$\frac{1}{3}$+lg$\frac{3}{5}$,k=5
满足条件S>-1,S=lg$\frac{1}{3}$+lg$\frac{3}{5}$+lg$\frac{5}{7}$,k=7
满足条件S>-1,S=lg$\frac{1}{3}$+lg$\frac{3}{5}$+lg$\frac{5}{7}$+lg$\frac{7}{9}$,k=9
满足条件S>-1,S=lg$\frac{1}{3}$+lg$\frac{3}{5}$+lg$\frac{5}{7}$+lg$\frac{7}{9}$+lg$\frac{9}{11}$=lg($\frac{1}{3}$×$\frac{3}{5}$×$\frac{5}{7}$×$\frac{7}{9}$×$\frac{9}{11}$)=lg$\frac{1}{11}$=-lg11,k=11
不满足条件S>-1,退出循环,输出k的值为11.
故选:C.
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)的图象关于x=$\frac{π}{3}$对称 | |
| C. | 函数f(x)的图象可由g(x)=2sin2x-1的图象向右平移$\frac{π}{6}$个单位得到 | |
| D. | 函数f(x)在区间[0,$\frac{π}{4}$]上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
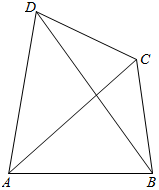 如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求
如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 8 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{4}{13}$,$\frac{1}{3}$] | B. | ($\frac{4}{13}$,$\frac{1}{3}$] | C. | (-∞,$\frac{1}{3}$] | D. | [$\frac{1}{3}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com