
分析 (Ⅰ)求函数的导数,利用导数的几何意义建立切线斜率关系进行求解即可.
(Ⅱ)利用作差法进行求解证明即可.
解答 解:(Ⅰ)∵函数f(x)=lnx的反函数为g(x).
∴g(x)=ex.,f(-x)=ln(-x),
则函数的导数g′(x)=ex,f′(x)=$\frac{1}{x}$,(x<0),
设直线m与g(x)相切与点(x1,${e}^{{x}_{1}}$),
则切线斜率k2=${e}^{{x}_{1}}$=$\frac{{e}^{{x}_{1}}}{{x}_{1}}$,则x1=1,k2=e,
设直线l与f(x)相切与点(x2,ln(-x2)),则切线斜率k1=$\frac{1}{{x}_{2}}$=$\frac{ln(-{x}_{2})}{{x}_{2}}$,则x2=-e,k1=-$\frac{1}{e}$,
故k2k1=-$\frac{1}{e}$×e=-1,则l⊥m.
(Ⅱ)不妨设a>b,
∵P-R=g($\frac{a+b}{2}$)-$\frac{g(a)+g(b)}{2}$=${e}^{\frac{a+b}{2}}$-$\frac{{e}^{a}+{e}^{b}}{2}$=-$\frac{({e}^{\frac{a}{2}}-{e}^{\frac{b}{2}})^{2}}{2}$<0,∴P<R,
∵P-Q=g($\frac{a+b}{2}$)-$\frac{g(a)-g(b)}{a-b}$=${e}^{\frac{a+b}{2}}$-$\frac{{e}^{a}-{e}^{b}}{a-b}$=$\frac{(a-b){e}^{\frac{a+b}{2}}-{e}^{a}+{e}^{b}}{a-b}$=$\frac{{e}^{\frac{a+b}{2}}(a-b-{e}^{\frac{a-b}{2}}+{e}^{\frac{b-a}{2}})}{a-b}$,
令φ(x)=2x-ex+e-x,则φ′(x)=2-ex-e-x<0,则φ(x)在(0,+∞)上为减函数,
故φ(x)<φ(0)=0,
取x=$\frac{a-b}{2}$,则a-b-${e}^{\frac{a-b}{2}}$+${e}^{\frac{b-a}{2}}$<0,∴P<Q,
$\frac{{e}^{a}+{e}^{b}}{2}>\frac{{e}^{a}-{e}^{b}}{a-b}$?$\frac{a-b}{2}>\frac{{e}^{a}-{e}^{b}}{{e}^{a}+{e}^{b}}$=$\frac{{e}^{a-b}-1}{{e}^{a-b}+1}$=1-$\frac{2}{{e}^{a-b}+1}$
令t(x)=$\frac{x}{2}$-1+$\frac{2}{{e}^{x}+1}$,
则t′(x)=$\frac{1}{2}$-$\frac{2{e}^{x}}{({e}^{x}+1)^{2}}$=$\frac{({e}^{x}-1)^{2}}{2({e}^{x}+1)^{2}}$≥0,
则t(x)在(0,+∞)上单调递增,
故t(x)>t(0)=0,
取x=a-b,则$\frac{a-b}{2}$-1+$\frac{2}{{e}^{a-b}+1}$>0,
∴R>Q,
综上,P<Q<R,
点评 本题主要考查导数的几何意义的应用以及利用作差法比较大小,考查学生的运算和推理能力,综合性较强,难度较大.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
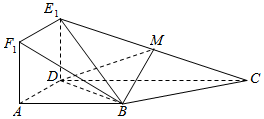 19、如图,在直角梯形ABCD中,AB∥CD,且AB=AD=2,CD=4,四边形ADE1F1是正方形,且平面ADE1F1⊥平面ABCD,M是E1C的中点.
19、如图,在直角梯形ABCD中,AB∥CD,且AB=AD=2,CD=4,四边形ADE1F1是正方形,且平面ADE1F1⊥平面ABCD,M是E1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m,n是异面直线,则α与β相交 | B. | 若m∥β,n∥α则α∥β | ||
| C. | 若m⊥n,则α⊥β | D. | 若m⊥β,则α⊥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com