
分析 (1)、根据题意,利用余弦的和差公式可得cos(α+β)=cosαcosβ-sinαsinβ,cos(α-β)=cosαcosβ+sinαsinβ,将两个式子相加,解可得证明;
(2)、根据题意,结合正弦定理可得S△ABC=$\frac{\sqrt{3}}{4}$sinBsinC,结合(1)的结论可得S△ABC=$\frac{2\sqrt{3}}{3}$[cos(2B-120°)+$\frac{1}{2}$],然后由△ABC为锐角三角形及B+C=120°可求B的范围,进而代入S△ABC=$\frac{2\sqrt{3}}{3}$[cos(2B-120°)+$\frac{1}{2}$],计算可得答案.
解答 解:(1)证明:cos(α+β)=cosαcosβ-sinαsinβ,
cos(α-β)=cosαcosβ+sinαsinβ,
sinαsinβ=$\frac{1}{2}$[(cosαcosβ+sinαsinβ)+(cosαcosβ-sinαsinβ)]=$\frac{1}{2}$[cos(α-β)-cos(α+β)];
即原等式可证;
(2)在锐角△ABC中,由正弦定理可得$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$,
所以S△ABC=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc=$\frac{\sqrt{3}}{4}$a2$\frac{sinBsinC}{si{n}^{2}A}$=$\frac{4\sqrt{3}}{3}$sinBsinC,
由(1)可知,sinαsinβ=$\frac{1}{2}$[cos(α-β)-cos(α+β)]
=$\frac{1}{2}$[cos(B-C)+$\frac{1}{2}$]=$\frac{1}{2}$[cos(2B-120°)+$\frac{1}{2}$];
故S△ABC=$\frac{2\sqrt{3}}{3}$[cos(2B-120°)+$\frac{1}{2}$],
0°<B<90°,0°<C<90°且B+C=120°,
则有30°<B<90°,
即30°<2B-30°<150°,
则$\frac{1}{2}$<sin(2B-30°)≤1,
又由S△ABC=$\frac{2\sqrt{3}}{3}$[cos(2B-120°)+$\frac{1}{2}$],
故$\frac{2\sqrt{3}}{3}$<S△ABC≤$\sqrt{3}$.
点评 本题(1)考查三角函数的恒等变换,(2)考查正弦定理的应用,关键要正确利用(1)的结论.


科目:高中数学 来源: 题型:选择题
| A. | n=2 | B. | n=3 | C. | n=2或n=3 | D. | n=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
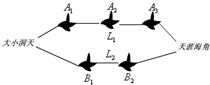 (理)“十一黄金周”期间三亚景区迎来了游客高峰期.游客小李从“大小洞天”到景区“天涯海角”景区有L1,L2两条路线(如图),路线L1上有A1,A2,A3三个风景点,各风景点遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1,B2两个风景点,各风景点遇到堵塞的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.
(理)“十一黄金周”期间三亚景区迎来了游客高峰期.游客小李从“大小洞天”到景区“天涯海角”景区有L1,L2两条路线(如图),路线L1上有A1,A2,A3三个风景点,各风景点遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1,B2两个风景点,各风景点遇到堵塞的概率依次为$\frac{3}{4}$,$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com