练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．设A={（x，y）|x≥0，y≥0，x+y≤1}，则区域{（x2，y2）|（x，y）∈A}的面积为1．

    分析 根据题意，求出A中x，y的取值集合，再由此求出区域{（x2，y2）|（x，y）∈A}的面积．

    解答 解：集合A={（x，y）|x≥0，y≥0，x+y≤1}表示的平面区域是如图所示的三角形OAB及其内部，
    则区域{（x2，y2）|（x，y）∈A}={（x2，y2）|$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\end{array}\right.$}={（s，t）|$\left\{\begin{array}{l}{0≤s≤1}\\{0≤t≤1}\end{array}\right.$}
    ∴该区域的面积为1×1=1．
    故答案为：1．

    点评 本题考查了二元一次不等式组表示平面区域的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．函数f（x）是定义域在R上的偶函数，且f（x）=-f（2-x），若f（x）在区间[1，2]上是减函数，则f（x）（　　）
    A．在区间[-2，-1]上是增函数，在区间[3，4]上是增函数
    B．在区间[-2，-1]上是增函数，在区间[3，4]上是减函数
    C．在区间[-2，-1]上是减函数，在区间[3，4]上是增函数
    D．在区间[-2，-1]上是减函数，在区间[3，4]上是减函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．若函数$f（x）={log_{\frac{1}{3}}}（{3{x^2}-ax+5}）$在[-1，+∞）上单调递减，则a的取值范围是（　　）
    A．（-∞，-6]B．[-8，-6）C．（-8，-6]D．[-8，-6]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知：命题p：?x∈R，x2+ax+1≥0，命题q：?x∈[-2，0]，x2-x+a=0，若命题p与命题q一真一假，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

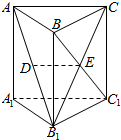    9．如图，在直三棱柱ABC-A1B1C1中，已知AC⊥BC，BC=CC1，设AB1的中点为D，BC1∩B1C=E．求证：
    （Ⅰ）DE∥平面AA1C1C；
    （Ⅱ）BC1⊥AB1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．抛物线x2=2y的焦点坐标为（　　）
    A．$（0，\frac{1}{2}）$B．$（\frac{1}{2}，0）$C．（0，1）D．（1，0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．偶函数f（x）在[0，6]上递减，那么f（-π）与f（5）大小关系是f（-π）＜f（5）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．若tanα=2，α是第三象限角，则sin（π+α）=$\frac{2\sqrt{5}}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．函数f（x）=tan（x+$\frac{π}{4}$）的单调增区间为（　　）
    A．（kπ-$\frac{π}{2}$，kπ+$\frac{π}{2}$），k∈ZB．（kπ，（k+1）π），k∈Z
    C．（kπ-$\frac{3π}{4}$，kπ+$\frac{π}{4}$），k∈ZD．（kπ-$\frac{π}{4}$，kπ+$\frac{3π}{4}$），k∈Z

    查看答案和解析>>

    同步练习册答案