
分析 (1)计算am,am+1+am+2,利用等差数列的性质计算公差d,再代入求和公式计算m;
(2)求出an,bn,得出数列{(an+6)•bn}的通项公式,利用错位相减法计算.
解答 解:(1)∵Sm-1=-4,Sm=0,Sm+2=14,
∴am=Sm-Sm-1=4,am+1+am+2=Sm+2-Sm=14.
设{an}的公差为d,则2am+3d=14,∴d=2.
∵Sm=$\frac{{a}_{1}+{a}_{m}}{2}×m$=0,∴a1=-am=-4.
∴am=a1+(m-1)d=-4+2(m-1)=4,
∴m=5.
(2)由(1)可得an=-4+2(n-1)=2n-6.
∵$\frac{{a}_{n}}{2}$=logabn,即n-3=logabn,
∴bn=an-3,
∴(an+6)•bn=2n•an-3,
设数列{(an+6)•bn}的前n项和为Tn,
则Tn=2•a-2+4•a-1+6•a0+8•a+…+2n•an-3,①
∴aTn=2•a-1+4•a0+6•a+8•a2+…+2n•an-2,②
①-②得:
(1-a)Tn=2a-2+2a-1+2a0+2a+…+2an-3-2n•an-2,
=$\frac{2{a}^{-2}(1-{a}^{n})}{1-a}$-2n•an-2
=$\frac{2{a}^{-2}}{1-a}$-$\frac{2(n-na+1){a}^{n-2}}{1-a}$,
∴Tn=$\frac{2{a}^{-2}}{(1-a)^{2}}$-$\frac{2(n-na+1){a}^{n-2}}{(1-a)^{2}}$.
点评 本题考查了等差数列,等比数列的性质,数列求和,属于中档题.


科目:高中数学 来源: 题型:解答题
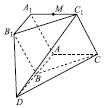 如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=$\frac{π}{3}$,M为棱A1C1的中点.
如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=$\frac{π}{3}$,M为棱A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{6}$ | B. | 1 | C. | $\frac{3}{4}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com