
| A�� | $\frac{27}{18}$ | B�� | $\frac{29}{18}$ | C�� | $\frac{17}{18}$ | D�� | $\frac{13}{18}$ |
���� ���õ������ε����ʽ����������������ʽ�������ʾΪ���ڦ˵Ĵ���ʽ��
�ٸ��ݻ�������ʽ����Сֵ���ɣ�
��� �⣺��ͼ��ʾ��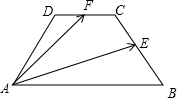
��������ABCD�У�AB��DC��AB=2��BC=1����ABC=60�㣬
����AD=BC=CD=1��
����$\overrightarrow{AE}$•$\overrightarrow{AF}$=��$\overrightarrow{AB}$+$\overrightarrow{BE}$��•��$\overrightarrow{AD}$+$\overrightarrow{DF}$��
=��$\overrightarrow{AB}$+��$\overrightarrow{BC}$��•��$\overrightarrow{AD}$+$\frac{1}{9��}$$\overrightarrow{DC}$��
=$\overrightarrow{AB}$•$\overrightarrow{AD}$+$\frac{1}{9��}$$\overrightarrow{AB}$•$\overrightarrow{DC}$+��$\overrightarrow{BC}$•$\overrightarrow{AD}$+$\frac{1}{9}$$\overrightarrow{BC}$•$\overrightarrow{DC}$
=2��1��cos60��+$\frac{1}{9��}$��2��1+�ˡ�1��1��cos60��+$\frac{1}{9}$��1��1��cos120��
=1+$\frac{2}{9��}$+$\frac{��}{2}$-$\frac{1}{18}$��$\frac{17}{18}$+2$\sqrt{\frac{2}{9��}•\frac{��}{2}}$=$\frac{29}{18}$��
���ҽ���$\frac{2}{9��}$=$\frac{��}{2}$������=$\frac{2}{3}$ʱ�Ⱥų�����
��ѡ��B��
���� ���⿼���˵������ε������Լ���������������ʽ���������⣬Ҳ�����˻�������ʽ����ֵ���⣮


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{5}$+$\frac{2}{5}$i | B�� | -$\frac{1}{5}$-$\frac{2}{5}$i | C�� | -$\frac{1}{3}$+$\frac{2}{3}$i | D�� | -$\frac{1}{3}$-$\frac{2}{3}$i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ���¾�Ҷͼ��¼�˼ס��������������3�β�ͬ�����еĵ÷�������ҶӼ�¼����һ������ģ������ȷ�ϣ�����������־�������ԣ�����ͼ����m��ʾ����ô��3�α����У��Ҷ�ƽ���÷ֳ�����ƽ���÷ֵĸ����ǣ�������
���¾�Ҷͼ��¼�˼ס��������������3�β�ͬ�����еĵ÷�������ҶӼ�¼����һ������ģ������ȷ�ϣ�����������־�������ԣ�����ͼ����m��ʾ����ô��3�α����У��Ҷ�ƽ���÷ֳ�����ƽ���÷ֵĸ����ǣ�������| A�� | $\frac{3}{5}$ | B�� | $\frac{4}{5}$ | C�� | $\frac{7}{10}$ | D�� | $\frac{9}{10}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com