
已知函数f(x)=x2-2acos kπ·ln x(k∈N*,a∈R,且a>0).
(1)讨论函数f(x)的单调性;
(2)若k=2 04,关于x的方程f(x)=2ax有唯一解,求a的值.
(1)当k是奇数时,f′(x)>0,则f(x)在(0,+∞)上是增函数;
当k是偶数时,f(x)在(0,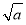 )上是单调减函数,在(
)上是单调减函数,在(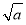 ,+∞)上是单调增函数.
,+∞)上是单调增函数.
(2)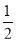
【解析】【解析】
(1)由已知得x>0
且f′(x)=2x-(-1)k·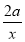 .
.
当k是奇数时,f′(x)>0,
则f(x)在(0,+∞)上是增函数;
当k是偶数时,
则f′(x)=2x-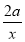 =
= .
.
所以当x∈(0,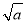 )时,f′(x)<0;
)时,f′(x)<0;
当x∈(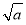 ,+∞)时,f′(x)>0.
,+∞)时,f′(x)>0.
故当k是偶数时,f(x)在(0,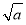 )上是单调减函数,在(
)上是单调减函数,在(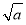 ,+∞)上是单调增函数.
,+∞)上是单调增函数.
(2)若k=2 014,
则f(x)=x2-2aln x(k∈N*).
记g(x)=f(x)-2ax=x2-2aln x-2ax,
则g′(x)=2x-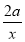 -2a=
-2a=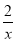 (x2-ax-a).
(x2-ax-a).
则方程f(x)=2ax有唯一解,即g(x)=0有唯一解.
令g′(x)=0,得x2-ax-a=0.
因为a>0,x>0,
所以x1=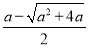 <0(舍去),
<0(舍去),
x2=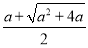 .
.
当x∈(0,x2)时,g′(x)<0,g(x)在(0,x2)上是单调减函数;当x∈(x2,+∞)时,g′(x)>0,g(x)在(x2,+∞)上是单调增函数.
当x=x2时,g′(x2)=0,g(x)min=g(x2).
因为g(x)=0有唯一解,所以g(x2)=0.则
 ,即
,即
两式相减得2aln x2+ax2-a=0,
因为a>0,所以2ln x2+x2-1=0.(*)
设函数h(x)=2lnx+x-1.
因为当x>0时,h(x)是增函数,所以h(x)=0至多有一个解.
因为h(1)=0,所以方程(*)的解为x2=1.
从而解得a=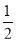 .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源:2015届高考苏教数学(理)训练17 任意角和弧度制及任意角的三角函数(解析版) 题型:填空题
已知角α和角β的终边关于直线y=x对称,且β=-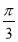 ,则sin α=______.
,则sin α=______.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:解答题
已知函数f(x)=x2-1与函数g(x)=aln x(a≠0).
(1)若f(x),g(x)的图像在点(1,0)处有公共的切线,求实数a的值;
(2)设F(x)=f(x)-2g(x),求函数F(x)的极值.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
定义在[1,+∞)上的函数f(x)满足:①f(2x)=cf(x)(c为正常数);②当2≤x≤4时,f(x)=1-|x-3|.若函数的所有极大值点均落在同一条直线上,则c=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练14 导数与函数单调性(解析版) 题型:填空题
函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f′(x)<0,设a=f(0),b=f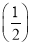 ,c=f(3),则a,b,c的大小关系为____________.
,c=f(3),则a,b,c的大小关系为____________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
设点P是曲线y=x2上的一个动点,曲线y=x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=x2的另一交点为Q,则PQ的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练10 对数与对数函数(解析版) 题型:填空题
函数y=loga(x-1)+1(a>0,且a≠1)的图像恒过定点A,若点A在一次函数y=mx+n的图像上,其中m,n>0,则 +
+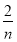 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破四 高考立体几何(解析版) 题型:解答题
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°.
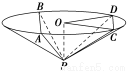
(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com