函数f(x)在定义域R内可导，若f(x)＝f(2－x)，且当x∈(－∞，1)时，(x－1)f′(x)<0，设a＝f(0)，b＝f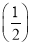
，c＝f(3)，则a，b，c的大小关系为____________．
科目：高中数学 来源：2015届高考苏教数学（理）训练4 函数及其表示（解析版） 题型：填空题
已知集合A＝[0,8]，集合B＝[0,4]，则下列对应关系中，不能看作从A到B的映射的是________．(填写序号)
①f：x→y＝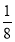
x ②f：x→y＝
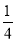x ③f：x→y＝
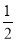x ④f：x→y＝x
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练16 导数与函数的综合问题（解析版） 题型：解答题
设f(x)是定义在区间(1，＋∞)上的函数，其导函数为f′(x)．如果存在实数a和函数h(x)，其中h(x)对任意的x∈(1，＋∞)都有h(x)＞0，使得f′(x)＝h(x)(x2－ax＋1)，则称函数f(x)具有性质P(a)．
(1)设函数f(x)＝ln x＋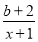
(x＞1)，其中b为实数．
①求证：函数f(x)具有性质P(b)；
②求函数f(x)的单调区间；
(2)已知函数g(x)具有性质P(2)．给定x1，x2∈(1，＋∞)，x1＜x2，设m为实数，α＝mx1＋(1－m)x2，β＝(1－m)x1＋mx2，且α＞1，β＞1，若|g(α)－g(β)|＜|g(x1)－g(x2)|，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练15 导数与函数极值、最值（解析版） 题型：填空题
设a>0，函数f(x)＝x＋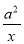
，g(x)＝x－ln x，若对任意的x1，x2∈[1，e]，都有f(x1)≥g(x2)成立，则实数a的取值范围为________．
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练14 导数与函数单调性（解析版） 题型：解答题
已知函数f(x)＝x2－2acos kπ·ln x(k∈N*，a∈R，且a>0)．
(1)讨论函数f(x)的单调性；
(2)若k＝2 04，关于x的方程f(x)＝2ax有唯一解，求a的值．
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练13 变化率与导数、导数的计算（解析版） 题型：填空题
已知函数f(x)＝ln x－f′(－1)x2＋3x－4，则f′(1)＝________.
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练11 函数与方程（解析版） 题型：填空题
若函数f(x)＝x3－ax2(a>0)在区间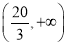
上是单调增函数，则使方程f(x)＝1 000有整数解的实数a的个数是________．
查看答案和解析>>
科目：高中数学 来源：2015届高考数学（理）一轮总复习专题突破四 高考立体几何（解析版） 题型：选择题
如图所示，ABCD－A1B1C1D1是棱长为6的正方体，E，F分别是棱AB，BC上的动点，且AE＝BF.当A1，E，F，C1共面时，平面A1DE与平面C1DF所成二面角的余弦值为( )
A.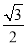
B.
C.
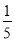D.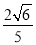
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
<1，因此有f(－1)<f(0)<f
，即有f(3)<f(0)<f
，c<a<b.
