
设f(x)是定义在区间(1,+∞)上的函数,其导函数为f′(x).如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得f′(x)=h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
(1)设函数f(x)=ln x+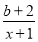 (x>1),其中b为实数.
(x>1),其中b为实数.
①求证:函数f(x)具有性质P(b);
②求函数f(x)的单调区间;
(2)已知函数g(x)具有性质P(2).给定x1,x2∈(1,+∞),x1<x2,设m为实数,α=mx1+(1-m)x2,β=(1-m)x1+mx2,且α>1,β>1,若|g(α)-g(β)|<|g(x1)-g(x2)|,求m的取值范围.
(1)当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为(1,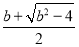 ),单调增区间为(
),单调增区间为(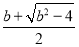 ,+∞).
,+∞).
(2)(0,1)
【解析】【解析】
(1)由f(x)=ln x+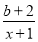 ,得f′(x)=
,得f′(x)=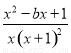 .
.
①证明:因为x>1时,h(x)=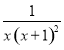 >0,所以函数f(x)具有性质P(b).
>0,所以函数f(x)具有性质P(b).
②当b≤2时,由x>1得x2-bx+1≥x2-2x+1=(x-1)2>0,
所以f′(x)>0.从而函数f(x)在区间(1,+∞)上单调递增.
当b>2时,令x2-bx+1=0得
x1=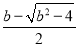 ,x2=
,x2=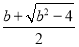 .
.
因为x1=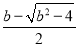 =
=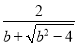 <
<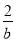 <1,
<1,
x2=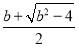 >1,
>1,
所以当x∈(1,x2)时,f′(x)<0;当x∈(x2,+∞)时,f′(x)>0;当x=x2时,f′(x)=0.从而函数f(x)在区间(1,x2)上单调递减,在区间(x2,+∞)上单调递增.
综上所述,当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为(1,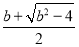 ),单调增区间为(
),单调增区间为(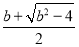 ,+∞).
,+∞).
(2)由题设知,g(x)的导函数
g′(x)=h(x)(x2-2x+1),
其中函数h(x)>0对于任意的x∈(1,+∞)都成立,
所以当x>1时,g′(x)=h(x)(x-1)2>0,
从而g(x)在区间(1,+∞)上单调递增.
①当m∈(0,1)时,
有α=mx1+(1-m)x2>mx1+(1-m)x1=x1,
α<mx2+(1-m)x2=x2,即α∈(x1,x2),
同理可得β∈(x1,x2).
所以由g(x)的单调性知g(α),g(β)∈(g(x1),g(x2)),从而有|g(α)-g(β)|<|g(x1)-g(x2)|,符合题意.
②当m≤0时,α=mx1+(1-m)x2≥mx2+(1-m)x2=x2,β=(1-m)x1+mx2≤(1-m)x1+mx1=x1,于是由α>1,β>1及g(x)的单调性知g(β)≤g(x1)<g(x2)≤g(α),
所以|g(α)-g(β)|≥|g(x1)-g(x2)|,与题意不符.
③当m≥1时,同理可得α≤x1,β≥x2,
进而得|g(α)-g(β)|≥|g(x1)-g(x2)|,与题意不符.
综上所述,所求的m的取值范围为(0,1).


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2015届高考苏教数学(理)训练6 函数的奇偶性及周期性(解析版) 题型:填空题
已知函数f(x)=x|x|-2x,则下列结论正确的是________.(填写序号)
①f(x)是偶函数,递增区间是(0,+∞)
②f(x)是偶函数,递减区间是(-∞,1)
③f(x)是奇函数,递减区间是(-1,1)
④f(x)是奇函数,递增区间是(-∞,0)
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练2 命题及其关系、充分条件与必要条件(解析版) 题型:填空题
命题“若实数a满足a≤2,则a2<4”的否命题是________命题(填“真”或“假”).
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练17 任意角和弧度制及任意角的三角函数(解析版) 题型:解答题
已知sin α<0,tan α>0.
(1)求α角的集合;
(2)求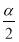 终边所在的象限;
终边所在的象限;
(3)试判断tan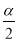 sin
sin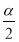 cos
cos 的符号.
的符号.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练17 任意角和弧度制及任意角的三角函数(解析版) 题型:填空题
已知角α和角β的终边关于直线y=x对称,且β=-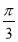 ,则sin α=______.
,则sin α=______.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:填空题
电动自行车的耗电量y与速度x之间有关系y= x3-
x3-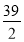 x2-40x(x>0),为使耗电量最小,则速度应定为________.
x2-40x(x>0),为使耗电量最小,则速度应定为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:解答题
已知函数f(x)=x2-1与函数g(x)=aln x(a≠0).
(1)若f(x),g(x)的图像在点(1,0)处有公共的切线,求实数a的值;
(2)设F(x)=f(x)-2g(x),求函数F(x)的极值.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练14 导数与函数单调性(解析版) 题型:填空题
函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f′(x)<0,设a=f(0),b=f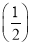 ,c=f(3),则a,b,c的大小关系为____________.
,c=f(3),则a,b,c的大小关系为____________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练1 集合(解析版) 题型:填空题
若集合P={x|3<x≤22},非空集合Q={x|2a+1≤x<3a-5},则能使Q⊆(P∩Q)成立的所有实数a的取值范围为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com