已知函数f(x)＝x|x|－2x，则下列结论正确的是________．(填写序号)
①f(x)是偶函数，递增区间是(0，＋∞)
②f(x)是偶函数，递减区间是(－∞，1)
③f(x)是奇函数，递减区间是(－1,1)
④f(x)是奇函数，递增区间是(－∞，0)
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案科目：高中数学 来源：2015届黑龙江哈尔滨第六中学高二下学期期中考试理科数学卷（解析版） 题型：选择题
采用系统抽样方法从960人中抽取32人做问卷调查．为此将他们随机编号为1,2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中，编号落入区间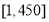
的人做问卷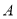
，编号落入区间
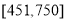的人做问卷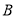
，其余的人做问卷
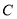，则抽到的人中，做问卷
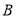的人数为( )
A．7 B．9 C．10 D．15
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练8 二次函数与幂函数（解析版） 题型：解答题
已知幂函数f(x)＝x(m2＋m)－1(m∈N*)，经过点(2，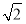
)，试确定m的值，并求满足条件f(2－a)>f(a－1)的实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练6 函数的奇偶性及周期性（解析版） 题型：解答题
设f(x)是(－∞，＋∞)上的奇函数，f(x＋2)＝－f(x)，
当0≤x≤1时，f(x)＝x.
(1)求f(3)的值；
(2)当－4≤x≤4时，求f(x)的图像与x轴所围成图形的面积．
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练5 函数的单调性与最值（解析版） 题型：填空题
定义在R上的函数f(x)满足f(x)＝f(x＋2)，当x∈[3,5]时，f(x)＝2－|x－4|.下列不等关系：
①
<
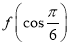；②f(sin l)>f(cos l)；
③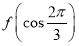
<
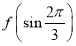；④f(cos 2)>f(sin 2)．
其中正确的是________(填序号)．
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练5 函数的单调性与最值（解析版） 题型：填空题
若f(x)＝－x2＋2ax与g(x)＝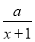
在区间[1,2]上都是减函数，则a的取值范围是________．
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练4 函数及其表示（解析版） 题型：填空题
已知集合A＝[0,8]，集合B＝[0,4]，则下列对应关系中，不能看作从A到B的映射的是________．(填写序号)
①f：x→y＝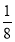
x ②f：x→y＝
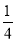x ③f：x→y＝
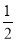x ④f：x→y＝x
查看答案和解析>>
科目：高中数学 来源：2015届高考苏教数学（理）训练16 导数与函数的综合问题（解析版） 题型：解答题
设f(x)是定义在区间(1，＋∞)上的函数，其导函数为f′(x)．如果存在实数a和函数h(x)，其中h(x)对任意的x∈(1，＋∞)都有h(x)＞0，使得f′(x)＝h(x)(x2－ax＋1)，则称函数f(x)具有性质P(a)．
(1)设函数f(x)＝ln x＋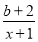
(x＞1)，其中b为实数．
①求证：函数f(x)具有性质P(b)；
②求函数f(x)的单调区间；
(2)已知函数g(x)具有性质P(2)．给定x1，x2∈(1，＋∞)，x1＜x2，设m为实数，α＝mx1＋(1－m)x2，β＝(1－m)x1＋mx2，且α＞1，β＞1，若|g(α)－g(β)|＜|g(x1)－g(x2)|，求m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，画出函数f(x)的图像，如图，观察图像可知，函数f(x)的图像关于原点对称，故函数f(x)为奇函数，且在(－1,1)上单调递减．
x＝
的解x0∈
，则正整数n＝________.