
分析 根据二次根式以及对数函数的性质得到关于x的不等式组,解出即可.
解答 解:由题意得:$\left\{\begin{array}{l}{2sinx-1>0}\\{1-2cosx≥0}\end{array}\right.$,
即:$\left\{\begin{array}{l}{sinx>\frac{1}{2}}\\{cosx≤\frac{1}{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{2kπ+\frac{π}{6}<x<2kπ+\frac{5π}{6}}\\{2kπ+\frac{π}{3}≤x≤2kπ+\frac{5π}{3}}\end{array}\right.$,k∈(z),
故函数的定义域是;[2kπ+$\frac{π}{3}$,2kπ+$\frac{5π}{6}$),(k∈z),
故答案为:[2kπ+$\frac{π}{3}$,2kπ+$\frac{5π}{6}$),(k∈z).
点评 本题考查了二次根式、对数函数以及三角函数的性质,是一道基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,$\frac{1}{e}$) | C. | (0,+∞) | D. | (0,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | $y=sin(2x+\frac{π}{8})$ | C. | y=cos2x | D. | $y=cos\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
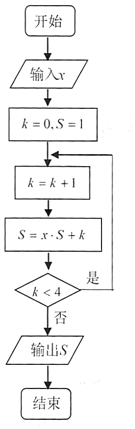 我国南宋数学家秦九韶(约公元1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0,当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0,然后进行求值.运行如图所示的程序框图,能求得多项式( )的值.
我国南宋数学家秦九韶(约公元1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0,当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0,然后进行求值.运行如图所示的程序框图,能求得多项式( )的值.| A. | x4+x3+2x2+3x+4 | B. | x4+2x3+3x2+4x+5 | C. | x3+x2+2x+3 | D. | x3+2x2+3x+4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com