
分析 (1)直接求和,可得结论;
(2)ak+ak+1=0,2a1=(1-2k)d,证明S2k-n-Sn=0即可.
解答 解:(1)对于数列①S1=5,S2=8,S4=8,S5=5;②S1=-14,S3=-30,S5=-30,S7=-14;
(2)∵ak+ak+1=0,2a1=(1-2k)d
S2k-n-Sn=(2k-n)a1+$\frac{(2k-n)(2k-n-1)}{2}$d-na1-$\frac{n(n-1)}{2}d$
=$\frac{d}{2}$[(2k-n)(1-2k)+(2k-n)(2k-n-1)-(1-2k)n-n(n-1)]
=$\frac{d}{2}$[2k-4k2-n+2nk+4k2-2kn-2k-2nk+n2+n-n+2kn-n2+n]
=$\frac{d}{2}$•0=0
点评 本题考查数列求和,考查归纳推理,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
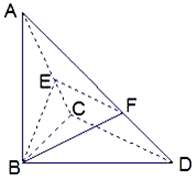 已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}$=λ(0<λ<1).
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}$=λ(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{16}$ | B. | $\frac{9}{2}$ | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com