
分析 运用换元法,令t=2x,t>0,则y=t2-3t+3,作出y=t2-3t+3在t>0的图象,求出y=1和y=7的交点,由题意可得[2,4]?[2a,4]?[3,4],可得a的不等式,解不等式可得所求范围.
解答 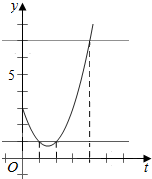 解:令t=2x,t>0,则y=t2-3t+3,
解:令t=2x,t>0,则y=t2-3t+3,
作出y=t2-3t+3在t>0的图象,
由x∈(-∞,0],可得t∈(0,1],
又x∈[a,2],可得t∈[2a,4],
由值域可得y的最小值我,最大值为7,
当t=3时,y=3,即有[2,4]?[2a,4]?[3,4],
即有2≤2a≤3,解得1≤a≤log23,
即有a的范围是[1,log23].
点评 本题考查可化为二次函数的值域问题,注意运用换元法,考查数形结合的思想方法,考查运算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
| 汽车排量 加油类型 | 小排量 | 大排量 |
| 92号 | 160 | 96 |
| 95号 | 20 | 24 |
| P(K2)≥k | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
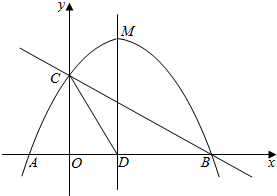 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
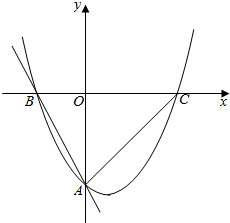 如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点
如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com