
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 先画出图象,结合图象以及椭圆的定义求出△FAB的周长的表达式,进而求出何时周长最大,求得m的值,求得A点坐标,利用kOA=kCD,即可求出和c的关系,求得椭圆的离心率.
解答 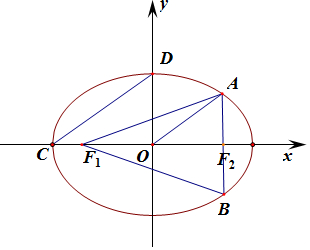
 解:设椭圆的右焦点F2.如图:
解:设椭圆的右焦点F2.如图:
由椭圆的定义得△FAB的周长为:
丨AB丨+丨AF丨+丨BF丨=丨AB丨+(2a-丨AF2丨)+(2a-丨BF2丨)=4a+丨AB丨-丨AF2丨-丨BF2丨;
∵丨AF2丨+丨BF2丨≥丨AB丨;
∴丨AB丨-丨AF2丨-丨BF2丨≤0,当AB过点F2时取等号;
∴△FAB的周长:丨AB丨+丨AF丨+丨BF丨=4a+丨AB丨-丨AF2丨-丨BF2丨≤4a;
∴△FAB的周长的最大值是4a,
则m=c,则A(c,$\frac{{b}^{2}}{a}$),
由CD∥OA,则kOA=kCD,即$\frac{\frac{{b}^{2}}{a}}{c}$=$\frac{b}{a}$,即b=c,
则a2=b2+c2=2c2,则a=$\sqrt{2}$c,
∴椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
故选:C.
点评 本题考查椭圆的标准方程及简单几何性质,直线的斜率公式,考查数形结合思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
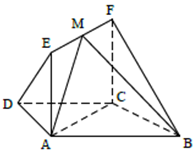 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (1,2] | C. | [2,4) | D. | (-4,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
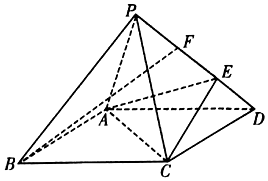 18、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.
18、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,$PB=PD=\sqrt{2}$,E为线段PD上一点,且PE=2ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com