
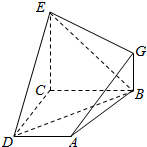
 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.分析 (1)取BE中点H,连结DH,则可证四边形ADHG为平行四边形,从而得到AG∥DH,推出AG∥平面BDE;
(2)将几何体分解成三棱锥A-BEG和四棱锥E-ABCD,分别求出他们的体积即可.
解答 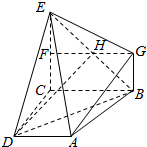 证明:(I)过G作GF⊥CE交BE于H,连结DH,则四边形BCFG是矩形,∴CF=BG,∴F是CE的中点,H是FG的中点,
证明:(I)过G作GF⊥CE交BE于H,连结DH,则四边形BCFG是矩形,∴CF=BG,∴F是CE的中点,H是FG的中点,
∴HG=$\frac{1}{2}BC$,HG∥BC,∵AD∥BC,AD=$\frac{1}{2}BC$,
∴AD=HG,AD∥HG,∴四边形ADHG是平行四边形,
∴AG∥DH,∵DH?平面BDE,AG?平面BDE,
∴AG∥平面BDE.
(II)连结AE,∵平面ABCD丄平面BCEG,平面ABCD∩平面BCEG=BC,∠BCD=∠BCE=$\frac{π}{2}$,
∴CE⊥平面ABCD,DC⊥平面BCEG,
∴由顶点ABCDEG所围成的几何体的体积V=V棱锥E-ABCD+V棱锥A-BEG
=$\frac{1}{3}×\frac{1}{2}(1+2)×2×2$+$\frac{1}{3}×\frac{1}{2}×1×2×2$=$\frac{8}{3}$.
点评 本题考查了线面平行的判定,面面垂直的性质,空间几何体的体积计算,属于中档题.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 “牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其主视图和侧视图完全相同时,它的俯视图可能是( )
“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其主视图和侧视图完全相同时,它的俯视图可能是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
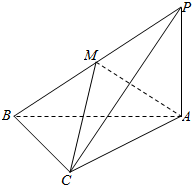 在三棱锥P-ABC中,∠PAB=∠PAC=∠ABC=90°,M是PB的中点,PA=AB=2.
在三棱锥P-ABC中,∠PAB=∠PAC=∠ABC=90°,M是PB的中点,PA=AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
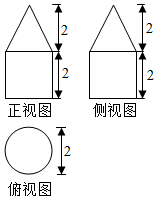
| A. | (5+$\sqrt{5}$)πcm2 | B. | (5+2$\sqrt{5}$)πcm2 | C. | (6+$\sqrt{5}$)πcm2 | D. | (6+2$\sqrt{5}$)πcm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com