
分析 (1)由题意设出直线l的方程,和抛物线联立后化为关于x的一元二次方程,由韦达定理得到A,B两点的横坐标的积,代入x1x2+y1y2中整理得到结果为0,所以结论得证.
(2)设A(x1,y1)、B(x2,y2),直线和x轴交点为N,利用S△OAB=$\frac{1}{2}$|ON|•|x1-x2|.求出直线的斜率,然后求出直线方程.
解答 (1)证明:由题意可知直线l的斜率存在,
设其斜率为k,则直线方程为:y=kx+4,
与抛物线方程联立,得$\left\{\begin{array}{l}{y=kx+4}\\{4y={x}^{2}}\end{array}\right.$,即x2-4kx-16=0,
设交点A,B的坐标分别为(x1,y1),(x2,y2),
所以x1x2=-16.x1+x2=4k,
则y1y2=k2x1x2+4k(x1+x2)+16=-16k2+16k2+16
可得x1x2+y1y2=0?OA⊥OB.
所以OA⊥OB.
(2)解:直线l过定点N(0,4),
∵S△OAB=S△OAN+S△OBN
=$\frac{1}{2}$|ON||x1|+$\frac{1}{2}$|ON||x2|
=$\frac{1}{2}$|ON|•|x1-x2|,
∴S△OAB=$\frac{1}{2}$•4•$\sqrt{({{x}_{1}+{x}_{2})}^{2}-4{x}_{1}{x}_{2}}$
=2$\sqrt{16{k}^{2}+64}$.
∵S△OAB=$12\sqrt{2}$,
∴2$\sqrt{16{k}^{2}+64}$=12$\sqrt{2}$.解得k=±$\frac{3\sqrt{2}}{2}$.
直线l的方程:y=±$\frac{3\sqrt{2}}{2}$x+4.
点评 本题考查的知识点是直线与圆锥曲线的关系,抛物线的应用,其中联立方程、设而不求、韦达定理三者综合应用是解答此类问题最常用的方法,但在解方程组时,是消去x还是消去y,这要根据解题的思路去确定.当然,这里消去x是最简捷的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
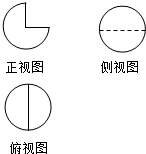 某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )
某几何体的三视图如图所示,其中俯视图与侧视图是半径均为$\sqrt{2}$的圆,则该几何体的表面积是( )| A. | 14π | B. | 12π | C. | 10π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
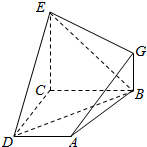 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com