
分析 (1)由离心率为方程2x2-5x+2=0的根,求出e,再由题意列a,b,c的等量关系列出方程组,求解即可得到椭圆的标准方程;
(2)由题意知直线AP,PB的斜率都存在,设P(m,n),设直线AP斜率为k,AP直线方程为:y=k(x+2),
联立$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,解得P点的坐标,又B(2,0),直线PB的斜率为$-\frac{3}{4k}$,求出PB直线方程为:$y=-\frac{3}{4k}(x-2)$,进一步求出M,N点的坐标,则线段MN的最小值可求.
解答 解:(1)∵2x2-5x+2=0的根为x=2或x=$\frac{1}{2}$,又离心率e∈(0,1),∴x=2舍去.
由题意列a,b,c的等量关系为:$\left\{\begin{array}{l}{a+c=3}\\{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}-{b}^{2}={c}^{2}}\end{array}\right.$,解得a=2,b=$\sqrt{3}$.
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由题意知直线AP,PB的斜率都存在,设P(m,n),设直线AP斜率为k,AP直线方程为:y=k(x+2),
联立$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得:(3+4k2)x2+16k2x+(16k2-12)=0,
则x1=-2,x2=m是其方程的两个根,∴-2m=$\frac{{16{k^2}-12}}{{3+4{k^2}}}$,
∴$m=\frac{6-8{k}^{2}}{3+4{k}^{2}}$,代入y=k(x+2),
得$n=\frac{12k}{3+4{k}^{2}}$,∴$P(\frac{6-8{k}^{2}}{3+4{k}^{2}},\frac{12}{3+4{k}^{2}})$,
又B(2,0)∴直线PB的斜率为$-\frac{3}{4k}$,
∴PB直线方程为:$y=-\frac{3}{4k}(x-2)$,
又直线AP,BP与直线x=4相交于M,N两点,
∴$M(4,6k),N(4,-\frac{3}{2k})$,$MN=|{6k}|+|{-\frac{3}{2k}}|$$≥2\sqrt{|{6k}|•|{-\frac{3}{2k}}|}=6$,
当且仅当$|{6k}|=|{-\frac{3}{2k}}|$时“=”成立,解得$k=±\frac{1}{2}$满足题意,
∴线段MN的最小值为6.
点评 本题考查了直线与圆锥曲线的关系,考查了椭圆的标准方程的求法,解答此题的关键是仔细计算,是中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -60 | B. | 70 | C. | -10 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
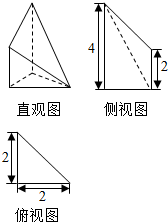 高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的( )
高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
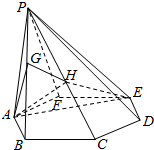 底面为正六边形的六棱锥P-ABCDE,$\overrightarrow{PG}$=$\frac{1}{2}$$\overrightarrow{GB}$,$\overrightarrow{PH}$=$\overrightarrow{HC}$,记三棱锥G-PAH的体积为V1,三棱锥H-PAE的体积为V2,则V1:V2是$\frac{1}{9}$.
底面为正六边形的六棱锥P-ABCDE,$\overrightarrow{PG}$=$\frac{1}{2}$$\overrightarrow{GB}$,$\overrightarrow{PH}$=$\overrightarrow{HC}$,记三棱锥G-PAH的体积为V1,三棱锥H-PAE的体积为V2,则V1:V2是$\frac{1}{9}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 “牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其主视图和侧视图完全相同时,它的俯视图可能是( )
“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其主视图和侧视图完全相同时,它的俯视图可能是( )| A. |  | B. | 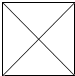 | C. | 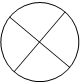 | D. | 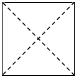 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com