
分析 先利用辅助角公式和m2+n2=1将函数f(x)化简为f(x)=ax+sin(x+φ),求出f′(x),根据f(x)的图象上存在两条切线垂直,不妨设在x=b与x=c处的切线互相垂直,则由导数的几何意义,分别求出两条切线的斜率k1=f′(b)=a+cos(b+φ),k2=f′(c)=a+cos(c+φ),则[a+cos(b+φ)][a+cos(c+φ)]=-1,化简为关于a的一元二次方程要有实数根,从而得到△≥0,再利用三角函数的有界性,即可得到cos(b+φ)=1,cos(c+φ)=-1或者cos(b+φ)=-1,cos(c+φ)=1,代入到[a+cos(b+φ)][a+cos(c+φ)]=-1,即可求出a=0.
解答 解:∵f(x)=ax+msinx+ncosx
∴f(x)=ax+$\sqrt{{m}^{2}+{n}^{2}}$sin(x+φ),
∵m2+n2=1,
∴f(x)=ax+sin(x+φ),
∴f′(x)=a+cos(x+φ),
∵f(x)=ax+msinx+ncosx的图象上存在两条切线垂直,
设在x=b与x=c处的切线互相垂直,
则k1=f′(b)=a+cos(b+φ),k2=f′(c)=a+cos(c+φ),
∴k1•k2=-1,
即[a+cos(b+φ)][a+cos(c+φ)]=-1,
∴关于a的二次方程a2+[cos(b+φ)+cos(c+φ)]a+cos(b+φ)cos(c+φ)+1=0有实数根,
∴△=[cos(b+φ)+cos(c+φ)]2-4×[cos(b+φ)cos(c+φ)+1]
=[cos(b+φ)-cos(c+φ)]2-4≥0,
又∵-2≤cos(b+φ)-cos(c+φ)≤2,
∴[cos(b+φ)-cos(c+φ)]2≤4,即[cos(b+φ)-cos(c+φ)]2-4≤0,
∴[cos(b+φ)-cos(c+φ)]2-4=0
∴cos(b+φ)=1,cos(c+φ)=-1或者cos(b+φ)=-1,cos(c+φ)=1,
∵[a+cos(b+φ)][a+cos(c+φ)]=-1,
∴a2-1=-1,
∴a=0,
故答案为:{0}.
点评 本题考查了利用导数研究曲线上某点切线方程,两直线垂直的条件.导数的几何意义即在某点处的导数即该点处切线的斜率,解题时要注意运用切点在曲线上和切点在切线上.属于中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=4x | B. | y=3x | C. | y=-3x | D. | y=-2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的正方体ABCD-A1B1C1D1中,
在如图所示的正方体ABCD-A1B1C1D1中,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
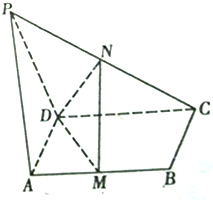 如图,已知PA⊥平面ABCD,ABCD为矩形,M、N为AB、PC的中点.
如图,已知PA⊥平面ABCD,ABCD为矩形,M、N为AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-1=0 | B. | x+y+1=0 | C. | x-y+1=0 | D. | x+y-1=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com