
分析 根据函数的解析式,利用变换法作出函数的图象.
解答 解:(1)把函数y=log${\;}_{\frac{1}{2}}$x的图象关于y轴对称,可得y=log${\;}_{\frac{1}{2}}$(-x)的图象,如图(1).
(2)把y=($\frac{1}{2}$)x的图象关于x轴对称,可得y=-($\frac{1}{2}$)x 的图象,如图(2)所示.
(3)把y=log2|x|的图象位于y轴右侧的保留,再把它的图象关于y轴对称,可得y=log2|x|的图象,
如图(3)所示.
(4)把y=|x2-1|的图象位于x轴上方的部分保留,把位于x轴下方的部分沿x轴对称到x轴的上方,
可得y=|x2-1|的图象,如图(4)所示.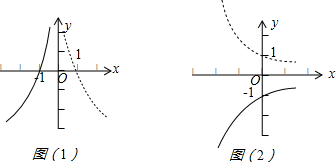
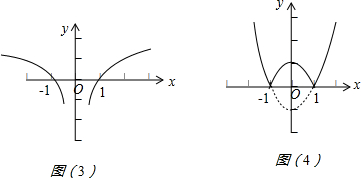
点评 本题主要考查用变换法进行作图,函数的图象的特征,属于中档题.


科目:高中数学 来源: 题型:填空题
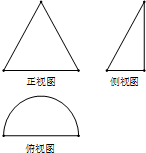 某几何体的三视图如图所示,其中正视图是腰长为2cm的等腰三角形,俯视图是半径为1cm的半圆,则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2,体积是$\frac{\sqrt{3}}{6}$πcm3.
某几何体的三视图如图所示,其中正视图是腰长为2cm的等腰三角形,俯视图是半径为1cm的半圆,则该几何体的表面积是$\frac{3π}{2}$+$\sqrt{3}$cm2,体积是$\frac{\sqrt{3}}{6}$πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ①③ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
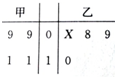 从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.
从巍山县庙街镇一所小学的甲、乙两个班级分别随机抽取4名学生的年龄制作出如右所示茎叶图,乙纪录中有一个数据模糊,无法确认,以X表示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com