练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．偶函数f（x）在（a＞0）上是单调函数，且f（0）f（a）＜0，则方程f（x）=0在区间[-a，a]内根的个数为2．

    分析 由条件f（0）•f（a）＜0可知，f（x）在（0，a）上有至少一个零点，又根据函数在（0，a）上单调，说明函数在（0，a）有且只有一个零点，再根据函数为偶函数，图象关于y轴对称，即可知函数在区间（-a，0）也有唯一零点，因此可以得出答案．

    解答 解：由二分法和函数的单调性可知：函数在区间[0，a]上有且只有一个零点，设为x=x0
    ∵函数是偶函数，
    ∴f（-x0）=f（x0）=0
    故其在对称区间[-a，0]上也有唯一零点，
    即函数在区间[-a，a]上存在两个零点，
    故答案为：2．

    点评 本题主要考查了函数零点的判定定理，属于基础题．灵活运用单调性和奇偶性以及函数的图象，有助于这类问题的解题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．作出下列各个函数图象的示意图：
    （1）y=log${\;}_{\frac{1}{2}}$（-x）；
    （2）y=-（$\frac{1}{2}$）x；
    （3）y=log2|x|；
    （4）y=|x2-1|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=$\frac{1}{2}$cos（2x-$\frac{π}{3}$）-$\frac{1}{2}$cos2x，x∈R．
    （1）求f（x）的最小正周期．
    （2）求f（x）在区间[-$\frac{π}{3}$，$\frac{π}{4}$]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．如图，ABCD-A1B1C1D1为正方体，则下列结论错误的是（　　）
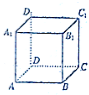
    A．A1C⊥B1D1B．B1D1∥平面BDC1
    C．A1C⊥平面BDC1D．异面直线AD与BC1所成的角为30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．（1）已知△ABC三个顶点坐标为A（2，-1），B（2，2），C（4，1），求三角形AC边上的中线所在直线方程；
    （2）倾斜角为60°且与直线5x-y+2=0有相同纵截距的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x（x-1），则x＜0时，f（x）的解析式为（　　）
    A．f（x）=x（x+1）B．f（x）=-x（x+1）C．f（x）=x（1-x）D．f（x）=x2-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知向量$\overrightarrow{OB}$=（2，0），向量$\overrightarrow{OC}$=（2，2），向量$\overrightarrow{CA}$=（$\sqrt{2}$cosα，$\sqrt{2}$sinα），则向量$\overrightarrow{OA}$与向量$\overrightarrow{CB}$的夹角的取值范围是[105°，165°]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知向量$\overrightarrow{a}$=（3，$\sqrt{3}$），$\overrightarrow{b}$=（-$\sqrt{3}$，1），则向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角大小是$\frac{2π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．若函数y=（$\frac{2}{2c+1}$）-x在R上单调递减，且函数g（x）=lg（2cx2+2x+1）的值域为R，则c的取值范围是0≤c＜$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案