
分析 (1)对函数f(x)求导后知g(x),对g(x)求导后得到单调性.
(2)利用导函数求得F(x)的单调性及最值,然后对a分情况讨论,利用F(x)无零点分别求得a的取值范围,再取并集即可.
解答 解:(1)$f'(x)={e^x}-\frac{1}{4},g(x)=xf'(x)=x({e^x}-\frac{1}{4})$,
∴$x>0,g'(x)=(x+1){e^x}-\frac{1}{4}>{e^x}-\frac{1}{4}>1-\frac{1}{4}=\frac{3}{4}>0$,
∴g(x)在(0,+∞)单调递增
(2)$F'(x)=\frac{1}{x}-af'(x)=\frac{{a(\frac{1}{a}-g(x))}}{x}$
又g(0)=0,g(x)在(0,+∞)单调递增,
∴存在唯一x0∈(0,+∞)使F'(x0)=0且x∈(0,x0),F'(x)>0,
x∈(x0,+∞),F'(x)<0,
∴F(x)在(0,x0)递增,(x0,+∞)递减,
∴Fmax(x)=F(x0)=lnx0-af(x0)+1,其中$a=\frac{1}{{g({x_0})}}$
又x→0+,F(x)→-∞,
∴F(x)=lnx-af(x)+1无零点等价于F(x0)<0
记$G(x)=lnx-\frac{f(x)}{g(x)}+1$,
∴$G'(x)=\frac{f(x)g'(x)}{{{g^2}(x)}}$
易知x>0时,f(x)>0,
∴G'(x)>0,
∴G(x)在(0,+∞)单调递增,且G(1)=0,
∴0<x0<1
又$\frac{1}{a}=g({x_0})∴0<\frac{1}{a}<e-\frac{1}{4}$,
∴$a>\frac{1}{{e-\frac{1}{4}}}$=$\frac{4}{4e-1}$,
故a的取值范围为($\frac{4}{4e-1}$,+∞)
点评 本题考查函数的综合应用,求极值和最值,主要考查求最值的方法和函数的单调性的运用,运用转化思想方法是解题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
第3个月 第4个月 | 租用a型车 | 租用b型车 |
| 租用a型车 | 60% | 50% |
| 租用b型车 | 40% | 50% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
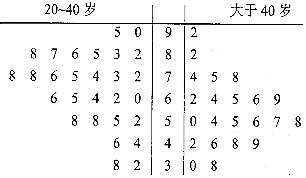 某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.| 购买意愿强 | 购买意愿弱 | 合计 | |
| 20-40岁 | |||
| 大于40岁 | |||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 2 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.
已知△ABC中,$AB=1,BC=\sqrt{3},BD$是AC边上的中线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=±\frac{{\sqrt{3}}}{3}x$ | B. | $y=±\sqrt{3}x$ | C. | $y=±\frac{1}{2}x$ | D. | y=±2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com