

分析 建立坐标系,求出平面AB1D的法向量$\overrightarrow{n}$和$\overrightarrow{BM}$的坐标,计算出$\overrightarrow{n}$和$\overrightarrow{BM}$的夹角即可得出结论.
解答 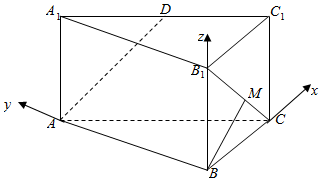 解:以BC,BA,BB1为坐标轴建立如图所示的坐标系.
解:以BC,BA,BB1为坐标轴建立如图所示的坐标系.
则A(0,2,0),B(0,0,0),C(2,0,0),A1(0,2,1),B1(0,0,1),C1(2,0,1),D(1,1,1),
∴$\overrightarrow{AD}$=(1,-1,1),$\overrightarrow{A{B}_{1}}$=(0,-2,1),$\overrightarrow{B{B}_{1}}$=(0,0,1),$\overrightarrow{{B}_{1}C}$=(2,0,-1),
∴$\overrightarrow{{B}_{1}M}$=$\frac{1}{3}\overrightarrow{{B}_{1}C}$=($\frac{2}{3}$,0,-$\frac{1}{3}$),∴$\overrightarrow{BM}$=$\overrightarrow{B{B}_{1}}$+$\overrightarrow{{B}_{1}M}$=($\frac{2}{3}$,0,$\frac{2}{3}$).
设面AB1D的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{B}_{1}}=0}\\{\overrightarrow{n}•\overrightarrow{AD}=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-2y+z=0}\\{x-y+z=0}\end{array}\right.$,令z=2得$\overrightarrow{n}$=(-1,1,2),
∴cos<$\overrightarrow{n}$,$\overrightarrow{BM}$>=$\frac{\overrightarrow{n}•\overrightarrow{BM}}{|\overrightarrow{n}||\overrightarrow{BM}|}$=$\frac{\frac{2}{3}}{\sqrt{6}•\frac{2\sqrt{2}}{3}}$=$\frac{\sqrt{3}}{6}$.
直线BM与面AB1D所成角的正弦值为$\frac{\sqrt{3}}{6}$.
点评 本题考查了空间向量在立体几何中的应用,线面角的计算,属于中档题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:选择题
| A. | y=-4x-1 | B. | y=4x-1 | C. | y=4x-11 | D. | y=-4x+7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移y(单位:cm)随时间t(单位:s)的变化曲线如图所示,则小球在开始振动(即t=0)时离开平衡位置的位移是3$\sqrt{3}$.
弹簧上挂着的小球做上下振动时,小球离开平衡位置的位移y(单位:cm)随时间t(单位:s)的变化曲线如图所示,则小球在开始振动(即t=0)时离开平衡位置的位移是3$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥m,l∥n,则m∥n | B. | 若l⊥α,n∥α,则l⊥n | C. | 若l⊥m,m∥n,则l⊥n | D. | 若l∥α,n∥α,则l∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com