练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求下列函数的导数：

    y＝；


     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如果数列a1，，，…，，…是首项为1，公比为－的等比数列，则a5＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}的公差大于0，且a3，a5是方程x2－14x＋45＝0的两根，数列{bn}的前n项的和为Sn，且Sn＝1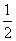－bn.

    (1)求数列{an}，{bn}的通项公式；

    (2)记cn＝an·bn，求证：cn＋1≤cn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数y＝ax3＋bx2＋cx＋d的图象与y轴交点为P，且曲线在P点处的切线方程为12x－y－4＝0. 若函数在x＝2处取得极值0，试确定函数的解析式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若曲线f(x)＝ax3＋lnx存在垂直于y轴的切线，则实数a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二次函数y＝f(x)的图象过原点，且它的导函数y＝f ′(x)的图象是过第一、二、三象限的一条直线，则函数y＝f(x)的图象的顶点在(　　)

    A．第一象限  B．第二象限

    C．第三象限  D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对正整数n，设曲线y＝xn(1－x)在x＝2处的切线与y轴交点的纵坐标为an，则数列的前n项和是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝ax3－2ax2＋b(a≠0)．

    (1)求出f(x)的极值；

    (2)若f(x)在区间[－2,1]上最大值是5，最小值是－11，求f(x)的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


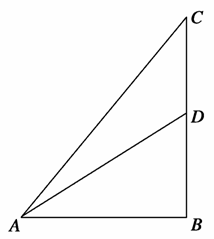
    一艘渔艇停泊在距岸9km处，今需派人送信给距渔艇3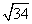km处的海岸渔站，如果送信人步行速度每小时5km，船行速度每小时4km，问应在何处登岸再步行可以使抵达渔站的时间最省？

    查看答案和解析>>

    同步练习册答案