
分析 (1)首先根据稳定函数的概念,可以采用赋值法,可得h(0)=0;
(2)根据“稳定函数”的定义,先满足②得a=2,然后检验函数g(x)=2x-1,是否满足理想函数的三个条件即可;
(3)根据“稳定函数”的定义进行推导即可.
解答 解:(1)取x1=x2=0,代入h(x1+x2)≥h(x1)+h(x2),可得h(0)≥h(0)+h(0)
即h(0)≤0,由已知?x∈[0,1],总有h(x)≥0可得h(0)≥0,
∴h(0)=0;
(2)若存在实数a,使得g(x)是稳定函数,
则若满足g(1)=1得g(1)=a-1=1,则a=2,
当a=2时,g(x)=2x-1,
①显然g(x)=2x-1在[0,1]上满足g(x)≥0;②g(1)=1.
若x1≥0,x2≥0,且x1+x2≤1,
则有g(x1+x2)-[g(x1)+g(x2)]=2x1+x2-1-[(2x1-1)+(2x2-1)]=(2x2-1)(2x1-1)≥0,
故g(x)=2x-1满足条件①②③,
即存在实数a=2,使得g(x)是稳定函数.
(3)由条件③知,任给m、n∈[0,1],当m<n时,由m<n知n-m∈[0,1],
∴f(n)=f(n-m+m)≥f(n-m)+f(m)≥f(m).
若f(x0)>x0,则f(x0)≤f[f(x0)]=x0,前后矛盾;
若:f(x0)<x0,则f(x0)≥f[f(x0)]=x0,前后矛盾.
故f(x0)=x0.
点评 本题主要考查抽象函数的应用,利用赋值法是解决抽象函数问题的常用方法,函数的新定义则转化为函数性质问题,本题则结合指数函数的性质,探讨函数的函数值域,指数函数的单调性的应用等知识点.综合性较强.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
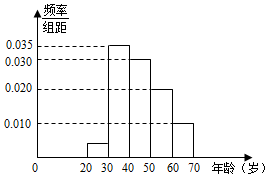 某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.
某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
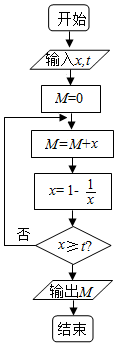
| A. | 3 | B. | $\frac{11}{3}$ | C. | $\frac{19}{6}$ | D. | $\frac{37}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com