
分析 (1)把已知数列递推式变形,可得$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}=2$(n≥2),由此说明数列$\{\frac{1}{S_n}\}$是以2为公差的等差数列;
(2)由(1)求出Sn,再由an=Sn-Sn-1(n≥2)求得数列{an}的通项公式.
解答 (1)证明:由an=$\frac{2S_n^2}{{2{S_n}-1}}$,得${S}_{n}-{S}_{n-1}=\frac{2{{S}_{n}}^{2}}{2{S}_{n}-1}$(n≥2),
即Sn-1-Sn=2SnSn-1,∴$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}=2$(n≥2).
∴数列$\{\frac{1}{S_n}\}$是以2为公差的等差数列;
(2)解:由(1)知,数列$\{\frac{1}{S_n}\}$是以2为公差的等差数列,又a1=$\frac{1}{2}$,
∴$\frac{1}{{S}_{1}}=2$,则$\frac{1}{{S}_{n}}=2+2(n-1)=2n$,
∴${S_n}=\frac{1}{2n}$.
则${a}_{n}={S}_{n}-{S}_{n-1}=\frac{1}{2n}-\frac{1}{2(n-1)}=-\frac{1}{2n(n-1)}$(n≥2).
∴${a_n}=\left\{\begin{array}{l}\frac{1}{2},(n=1)\\-\frac{1}{2n(n-1)},(n≥2)\end{array}\right.$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了等差数列通项公式的求法,是中档题.


科目:高中数学 来源: 题型:选择题
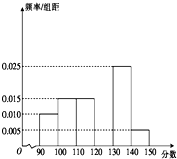 某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如图所示的频率分布直方图,则估计本次考试的平均分为( )
某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如图所示的频率分布直方图,则估计本次考试的平均分为( )| A. | 121 | B. | 119 | C. | 118.5 | D. | 118 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com