练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x≤4}\\{y≥3}\\{\;}\end{array}\right.$所表示的平面区域的面积为（　　）
    A．1B．2C．3D．4

    分析 作出不等式对应的平面区域，根据平面区域的形状确定平面区域的面积．

    解答 解：不等式组对应的平面区域如图
    则对应区域为直角三角形ABC．
    则三点坐标分别为A（2，3），B（4，3），C（4，5），
    则AB=2，BC=2，
    所以三角形的面积为S=$\frac{1}{2}$×2×2=2．
    故选：B．

    点评 本题主要考查二元一次不等式组表示平面区间，考查学生的作图能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．下列说法正确的是（　　）
    A．函数y=2x2-x+1在（0，+∞）上是增函数
    B．幂函数在（0，+∞）上都是增函数
    C．函数y=log2（x+$\sqrt{{x}^{2}+1}$）既不是奇函数，也不是偶函数
    D．已知f（x）是定义在R上的增函数，若a+b＞0，则有f（a）+f（b）＞f（-a）+f（-b）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．为了增强环保意识，某校从男生中随机制取了60人，从女生中随机制取了50人参加环保知识测试，统计数据如表所示，经计算K2=7.822，则环保知识是否优秀与性别有关的把握为（　　）
    优秀非优秀总计
    男生402060
    女生203050
    总计6050110
    附：x2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+{n}_{+1}{n}_{+2}}$
    P（K2≥k）0.5000.1000.0500.0100.001
    k0.4552.7063.8416.63510.828
    A．90%B．95%C．99%D．99.9%

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．计算：cos24°cos36°-cos66°cos54°=（　　）
    A．0B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）=$\left\{\begin{array}{l}-{x^2}+2x，x≤0\\ ln（x+1），x＞0\end{array}\right.$，若对x∈R都有|f（x）|≥ax，则实数a的取值范围是（　　）
    A．（-∞，0]B．[-2，0]C．[-2，1]D．（-∞，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

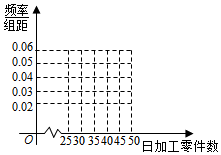    15．随机观测生产某种们零件的某工厂20名工人的日加工零件数（单位：件），获得数据如下：30，42，41，36，44，48，37，25，45，43，31，49，34，33，43，38，32，46，39，36．根据上述数据得到样本的频率分布表如下：
    分组频数频率
    [25，30]20.10
    （30，35]40.20
    （35，40]50.25
    （40，45]mfm
    （45，50]nfn
    （1）确定样本频率分布表中m，n，fm和fn的值；
    （2）根据上述频率分布表，画出样本频率分布直方图；
    （3）根据样本频率分布直方图，求在该厂任取3人，至少有1人的日加工零件数落在区间（30，35]的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．若$|{\begin{array}{l}{2^x}&1\\ 3&{2^x}\end{array}}|=0$，则x的值是${log}_{2}\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设定义在D上的函数y=h（x）在点P（x0，h（x0）处的切线方程为l：y=g（x），当x≠x0时，若$\frac{h（x）-g（x）}{x-{x}_{0}}$＞0在D内恒成立，则称P为函数y=h（x）的“类对称点”，则f（x）=lnx+2x2-x的“类对称点”的横坐标是（　　）
    A．eB．$\frac{1}{2}$C．$\sqrt{2}$D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．单位向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|3$\overrightarrow{a}$-4$\overrightarrow{b}$|=5，则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=（　　）
    A．3B．$\sqrt{3}$C．5D．$\sqrt{5}$

    查看答案和解析>>

    同步练习册答案