考点:用空间向量求平面间的夹角,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明:平面A
1BE⊥平面B
1CD,只需要证明BE⊥平面B
1CD即可;
(Ⅱ)以D为坐标原点,建立坐标系,设AB=a,求出平面A
1BE的法向量,底面A
1B
1C
1D
1的法向量,利用向量的夹角公式,结合
<AB<2,即可求θ的取值范围.
解答:
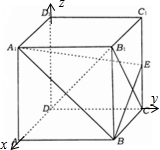
(Ⅰ)证明:∵CD⊥平面BCC
1B
1,
∴CD⊥BE,
∵E为CC
1的中点,
∴△B
1BC∽△BCE,
∴∠EBC=∠BB
1C,
∴∠EBB
1+∠BB
1C=90°,
∴BE⊥B
1C,
∴B
1C∩CD=C,
∴BE⊥平面B
1CD,
∵BE?平面A
1BE,
∴平面A
1BE⊥平面B
1CD;
(Ⅱ)解:以D为坐标原点,建立坐标系,设AB=a,则
A
1(
,0,2),B(
,a,0),E(0,a,1),
∴
=(0,a,-2),
=(-
,a,-1),
设平面A
1BE的法向量为
=(x,y,z),则
,
∴可取
=(
,1,
)
∵底面A
1B
1C
1D
1的法向量为
=(0,0,1),
∴cosθ=
=
,
∵
<AB<2,
∴
<a2<8,
∴
<
<2,
∴
<cosθ<,
∴
<θ<.
点评:本题考查线面、面面垂直,考查空间角,考查向量知识的运用,知识综合性强.

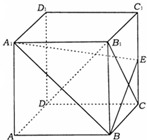 长方体ABCD-A1B1C1D1中,AA1=2,BC=
长方体ABCD-A1B1C1D1中,AA1=2,BC= (Ⅰ)证明:∵CD⊥平面BCC1B1,
(Ⅰ)证明:∵CD⊥平面BCC1B1,
