
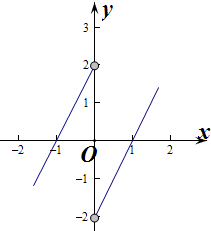
| 1 |
| 10 |
| 1 |
| 10 |
| 1 |
| 10 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 为考察中学生的性别与是否喜欢某项运动之间的关系,随机抽取了某校的部分学生进行调查,并将调查数据制作成二维条形图(如图),若已知共有83名学生喜欢此项运动,且男生的喜欢比例比女生多29%,则女生中喜欢此项运动的比例是( )
为考察中学生的性别与是否喜欢某项运动之间的关系,随机抽取了某校的部分学生进行调查,并将调查数据制作成二维条形图(如图),若已知共有83名学生喜欢此项运动,且男生的喜欢比例比女生多29%,则女生中喜欢此项运动的比例是( )| A、35% | B、36% |
| C、64% | D、65% |
查看答案和解析>>
科目:高中数学 来源: 题型:
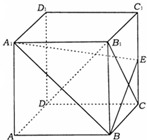 长方体ABCD-A1B1C1D1中,AA1=2,BC=
长方体ABCD-A1B1C1D1中,AA1=2,BC=| 2 |
2
| ||
| 5 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com