
分析 (1)利用条件求数列的首项和公差,公比,然后求等差数列和等比数列的通项公式.
(2)利用错位相减法即可求出数列{cn}的前n项和,
(3)利用放缩法得到$\sqrt{\frac{1}{{a}_{n}+2}}$>$\sqrt{2n+1}$-$\sqrt{2n-1}$,再求和,需要验证n=2,3是否成立,问题得以证明.
解答 解:(1)∵Sn=2(bn-1),①
∴当n≥2时,Sn-1=2(bn-1-1),②
由①-②得:bn=2(bn-bn-1)(n≥2),即bn=2bn-1(n≥2),
又n=1时,S1=2(b1-1),得b1=2,
∴${b_n}={2^n}$(n∈N*).
设数列{an}的公差为d,则$d=\frac{{{a_5}-{a_2}}}{5-2}=2$,
所以an=2n-3(n∈N*).
(2)由(1)知${c_n}=(2n-3)•{2^n}$,设数列{cn}的前n项和为Tn,
则${T_n}=-1×2+1×{2^2}+3×{2^3}+…+(2n-3)×{2^n}$,
$2{T_n}=-1×{2^2}+1×{2^3}+3×{2^4}+…+(2n-5)×{2^n}+(2n-3)×{2^{n+1}}$,
两式作差得$-{T_n}=-1×2+2×{2^2}+2×{2^3}+…+2×{2^n}-(2n-3)×{2^{n+1}}$=$-2-\frac{{8(1-{2^{n+1}})}}{1-2}-(2n-3)×{2^{n+1}}$=-10-(2n-5)×2n+1,
∴${T_n}=(2n-5)•{2^{n+1}}+10$(n∈N*).
(3)证明:∵$\sqrt{\frac{1}{{a}_{n}+2}}$=$\frac{1}{\sqrt{2n-1}}$=$\frac{2}{\sqrt{2n-1}+\sqrt{2n+1}}$>$\frac{2}{\sqrt{2n-1}+\sqrt{2n+1}}$=$\sqrt{2n+1}$-$\sqrt{2n-1}$,
∴$\sqrt{\frac{1}{{{a_1}+2}}}+\sqrt{\frac{1}{{{a_2}+2}}}+…+\sqrt{\frac{1}{{{a_n}+2}}}>(\sqrt{3}-1)+(\sqrt{5}-\sqrt{3})+…+(\sqrt{2n+1}-\sqrt{2n-1})=\sqrt{2n+1}-1$,
又∵$(\sqrt{2n+1}-1)-\sqrt{n}=\sqrt{2n+1}-(\sqrt{n}+1)$,
且当n≥4时,${(\sqrt{2n+1})^2}-{(\sqrt{n}+1)^2}=n-2\sqrt{n}=\sqrt{n}(\sqrt{n}-2)≥0$,
∴$\sqrt{2n+1}-1≥\sqrt{n}$,
∴当n≥4时,$\sqrt{\frac{1}{{{a_1}+2}}}+\sqrt{\frac{1}{{{a_2}+2}}}+…+\sqrt{\frac{1}{{{a_n}+2}}}>\sqrt{n}$成立,
当n=2,n=3时,可以验证不等式也成立.
综上,当n≥2时,$\sqrt{\frac{1}{{{a_1}+2}}}+\sqrt{\frac{1}{{{a_2}+2}}}+…+\sqrt{\frac{1}{{{a_n}+2}}}>\sqrt{n}$.
点评 本题主要考查等差数列和等比数列的通项公式,以及利错位相减法求前n项和Sn,放缩法证明不等式成立,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,△ABC是圆O的内接三角形,P是BA的延长线上一点,且PC切圆O于点C.
如图,△ABC是圆O的内接三角形,P是BA的延长线上一点,且PC切圆O于点C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
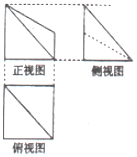 已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )
已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )| A. | 3 | B. | $\frac{10}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题?x0∈R,x${\;}_{0}^{2}$+1>3x0的否定是:?x∈R,x2+1<3x | |
| B. | 命题△ABC中,若A>B,则cosA>cosB的否命题是真命题 | |
| C. | 平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是钝角的充要条件是:$\overrightarrow{a}$•$\overrightarrow{b}$<0 | |
| D. | ω=1是函数f(x)=sinωx-cosωx的最小正周期为2π的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com