
【题目】设定义在R上的偶函数y=f(x),满足对任意t∈R都有f(t)=f(2﹣t),且x∈(0,1]时,f(x)= ![]() ,a=f(
,a=f( ![]() ),b=f(
),b=f( ![]() ),c=f(
),c=f( ![]() ),则( )
),则( )
A.b<c<a
B.a<b<c
C.c<a<b
D.b<a<c
【答案】C
【解析】解:∵定义在R上的偶函数y=f(x),满足对任意t∈R都有f(t)=f(2﹣t),
∴f(2+t)=f(2﹣2﹣t)=f(﹣t)=f(t),
∴f(x)是以2为周期的函数,
∵x∈[0,1]时,f(x)= ![]() ,
,
f′(x)= ![]() ≥0在[0,1]恒成立,
≥0在[0,1]恒成立,
故f(x)在[0,1]递增,
由a=f( ![]() )=f(1+
)=f(1+ ![]() )=f(﹣
)=f(﹣ ![]() )=f(
)=f( ![]() ),
),
b=f( ![]() )=f(1+
)=f(1+ ![]() )=f(﹣
)=f(﹣ ![]() )=f(
)=f( ![]() ),
),
c=f( ![]() )=f(
)=f( ![]() ),
),
∴c<a<b,
故选:C.
【考点精析】利用函数的值对题目进行判断即可得到答案,需要熟知函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.


科目:高中数学 来源: 题型:
【题目】为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆): 147 161 170 180 163 172 178 167 191 182
181 173 174 165 158 154 159 189 168 169
(Ⅰ)完成如下频数分布表,并作频率分布直方图;
通行数量区间 | [145,155) | [155,165) | [165,175) | [175,185) | [185,195) |
频数 |
(Ⅱ)现用分层抽样的方法从通行数量区间为[165,175)、[175,185)及[185,195)的路段中取出7处加以优化,再从这7处中随机选2处安装智能交通信号灯,设所取出的7处中,通行数量区间为[165,175)路段安装智能交通信号灯的数量为随机变量X(单位:盏),试求随机变量X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列条件求圆的方程.
(![]() )
)![]() ,
, ![]() ,
, ![]() ,三角形
,三角形![]() 的外接圆.
的外接圆.
(![]() )圆心在直线
)圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() .
.
(![]() )与
)与![]() 轴相切,圆心在直线
轴相切,圆心在直线![]() 上,且被直线
上,且被直线![]() 截得的弦长为
截得的弦长为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电力公司为了制定节电方案,需要了解居民用电情况.通过随机抽样,电力公司获得了50户居民的月平均用电量,分为六组制出频率分布表和频率分布直方图(如图所示).


(1)求a,b的值;
(2)为了解用电量较大的用户用电情况,在第5、6两组用分层抽样的方法选取5户 .
①求第5、6两组各取多少户?
②若再从这5户中随机选出2户进行入户了解用电情况,求这2户中至少有一户月平均用电量在[1000,1200]范围内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5.同时投掷这两枚玩具一次,记![]() 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和.
(Ⅰ)求事件“m不小于6”的概率;
(Ⅱ)“m为奇数”的概率和“m为偶数”的概率是不是相等?证明你作出的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°. 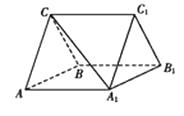
(1)证明:AB⊥A1C;
(2)若AB=CB=2,A1C= ![]() ,求二面角B﹣AC﹣A1的余弦值.
,求二面角B﹣AC﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=a,BC=1,∠BAD=60°,E为线段CD(端点C、D除外)上一动点,将△ADE沿直线AE翻折,在翻折过程中,若存在某个位置使得直线AD与BC垂直,则a的取值范围是( ) 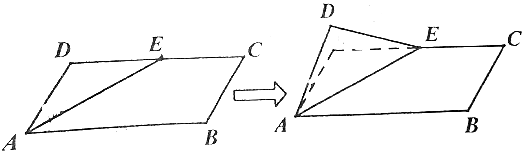
A.( ![]() ,+∞)
,+∞)
B.( ![]() ,+∞)
,+∞)
C.( ![]() +1,+∞)
+1,+∞)
D.( ![]() +1,+∞)
+1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() .过定点
.过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,
, ![]() (点
(点![]() 在点
在点![]() ,
, ![]() 之间).
之间).
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若射线![]() 交椭圆
交椭圆![]() 于点
于点![]() (
(![]() 为原点),求
为原点),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com