练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在平行四边形ABCD中，AB=a，BC=1，∠BAD=60°，E为线段CD（端点C、D除外）上一动点，将△ADE沿直线AE翻折，在翻折过程中，若存在某个位置使得直线AD与BC垂直，则a的取值范围是（ ）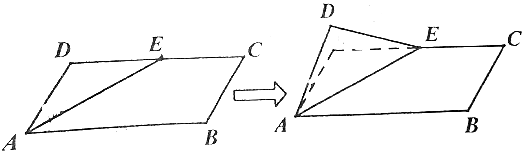

    A.（ ，+∞）
    B.（ ，+∞）
    C.（ +1，+∞）
    D.（ +1，+∞）

    【答案】D
    【解析】解：设翻折前的D记为D′，∵AD⊥BC，BC∥AD′，则在翻折过程中，存在某个位置使得直线AD与BC垂直，只需保证∠DAD′=900 ， ∵∠D′AE=∠DAE，由极限位置知，只需保证∠D′AE≥45°即可．
    在△D′AE中，AD′=1，∠D′AE=45°，∠AD′E=120°，则∠D′EA=15°，
    由正弦定理知， ，则D′E= ．
    因为E为线段CD（端点C，D除外）上的一动点，
    则a＞ ，
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在三棱锥A﹣BCD中，侧棱AB，AC，AD两两垂直，△ABC、△ACD、△ABD的面积分别为 、 、2 ，则三棱锥A﹣BCD的外接球的体积为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设定义在R上的偶函数y=f（x），满足对任意t∈R都有f（t）=f（2﹣t），且x∈（0，1]时，f（x）= ，a=f（ ），b=f（ ），c=f（ ），则（ ）
    A.b＜c＜a
    B.a＜b＜c
    C.c＜a＜b
    D.b＜a＜c

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数,其中为正实数．

    (1)若函数在处的切线斜率为2，求的值；

    (2)求函数的单调区间；

    (3)若函数有两个极值点，求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】输入x，求函数y＝的值的程序框图如图C17所示．

    (1)指出程序框图中的错误之处并写出正确的算法步骤．

    (2)重新绘制程序框图，并回答下面提出的问题．

    ①要使输出的值为7，则输入的x的值应为多少？

    ②要使输出的值为正数，则输入的x应满足什么条件？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体的棱长为， 为的中点， 为线段上的动点，过点， ， 的平面截该正方体所得的截面为，则下列命题正确的是__________（写出所有正确命题的编号）.

    ①当时， 为四边形；②当时， 为等腰梯形；

    ③当时， 与的交点满足；

    ④当时， 为五边形；

    ⑤当时， 的面积为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，正方形与直角梯形所在平面互相垂直， ， ， ．

    （I）求证： 平面．

    （II）求证： 平面．

    （III）求四面体的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，设动点到两定点， 的距离的比值为的轨迹为曲线．

    （Ⅰ）求曲线的方程；

    （Ⅱ）若直线过点，且点到直线的距离为，求直线的方程，并判断直线与曲线的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两人相约于下午1：00～2：00之间到某车站乘公共汽车外出，他们到达车站的时间是随机的．设在下午1：00～2：00之间该车站有四班公共汽车开出，开车时间分别是1：15，1：30，1：45，2：00.求他们在下述情况下乘同一班车的概率：

    (1)约定见车就乘；

    (2)约定最多等一班车．

    查看答案和解析>>

    同步练习册答案