Question

14．长方体ABCD-A₁B₁C₁D₁中，$A{A_1}=\sqrt{2}$，AB=1，AD=2，E为BC的中点．设△A₁DE的重心为G，问是否存在实数λ，使得$\overrightarrow{AM}=λ\overrightarrow{AD}$，且MG⊥平面A₁DE同时成立？若存在，求出λ的值；若不存在，说明理由．

Answer 1

分析 过G作GM∥AH交AD于M，由AH⊥面A₁DE得到MG⊥面A₁DE，再利用重心的性质及平行线截线段成比例定理得到λ的值．

解答 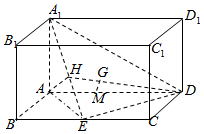解：存在实数$λ=\frac{1}{3}$，使得$\overrightarrow{AM}=λ\overrightarrow{AD}$，
且MG⊥平面A₁DE同时成立
理由如下：由题意求得AE=$\sqrt{2}$，DE=$\sqrt{2}$，
又AD=2，∴AE²+ED²=AD²，∴AE⊥DE．
又DE⊥AA₁，AA₁∩AE=A，AA₁?面A₁AE，
AE?面A₁AE，
∴DE⊥面A₁AE，∴平面A₁AE⊥平面A₁ED，
∵AA₁=AE=$\sqrt{2}$，
取A₁E的中点H，AH⊥A₁E，AH⊥DE，A₁E∩ED=E，A₁E?面A₁DE，
 ED?面A₁DE，∴AH⊥面A₁DE，
在三角形A₁ED中，∵H是A₁E的中点，G为三角形A₁ED的重心，
又∵AH⊥面A₁ED，过点G作GM∥AH交AD于M，
则MG⊥A₁ED，且AM=$\frac{1}{3}AD$，
故存在实数$λ=\frac{1}{3}$，使得$\overrightarrow{AM}=λ\overrightarrow{AD}$，且MG⊥平面A₁DE同时成立．

点评 本题考查了直线与平面平行的判定定理的应用，考查空间想象能力以及逻辑推理能力、转化思想的应用．属于中档题．