
| 年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 人数 | 4 | 5 | 8 | 5 | 3 |
| 年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
| 人数 | 6 | 7 | 3 | 5 | 4 |
分析 (I)设“年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休””为事件A,则P(A)=$\frac{{∁}_{3}^{2}}{{∁}_{5}^{2}}$.
(II)X的可能取值为0,1,2,3.利用相互独立与互斥事件的概率计算公式即可得出.
解答 解:(I)设“年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休””为事件A,
则P(A)=$\frac{{∁}_{3}^{2}}{{∁}_{5}^{2}}$=$\frac{3}{10}$.
(II)X的可能取值为0,1,2,3.P(X=0)=$\frac{{∁}_{3}^{2}{∁}_{2}^{2}}{{∁}_{5}^{2}•{∁}_{3}^{2}}$=$\frac{1}{10}$,
P(X=1)=$\frac{{∁}_{3}^{1}{∁}_{2}^{1}{∁}_{2}^{2}+{∁}_{3}^{2}{∁}_{2}^{1}{∁}_{1}^{1}}{{∁}_{5}^{2}{∁}_{3}^{2}}$=$\frac{2}{5}$.P(X=2)=$\frac{{∁}_{2}^{2}{∁}_{2}^{2}+{∁}_{3}^{1}{∁}_{2}^{1}{∁}_{2}^{1}{∁}_{1}^{1}}{{∁}_{5}^{2}{∁}_{3}^{2}}$=$\frac{13}{30}$,
P(X=3)=$\frac{{∁}_{2}^{2}{∁}_{2}^{1}{∁}_{1}^{1}}{{∁}_{5}^{2}{∁}_{3}^{2}}$=$\frac{1}{15}$.X的分布列如下:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{10}$ | $\frac{2}{5}$ | $\frac{13}{30}$ | $\frac{1}{15}$ |
点评 本题考查了相互独立与互斥事件的概率计算公式、随机变量的分布列与数学期望,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
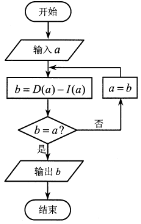 设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,
设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=f(x+π) | B. | f(x)=f(x+$\frac{π}{2}$) | C. | f(x)=f($\frac{π}{3}$-x) | D. | f(x)=f($\frac{π}{6}$-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在矩形ABCD中,$AB=3,AD=3\sqrt{2}$,点E为BC的中点,如果DF=2FC,那么$\overrightarrow{AF}•\overrightarrow{BE}$的值是9.
如图,在矩形ABCD中,$AB=3,AD=3\sqrt{2}$,点E为BC的中点,如果DF=2FC,那么$\overrightarrow{AF}•\overrightarrow{BE}$的值是9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com