
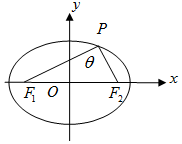
 椭圆$\frac{x^2}{4}+{y^2}$=1上的一点P与两焦点F1,F2所构成的三角形称为焦点三角形.
椭圆$\frac{x^2}{4}+{y^2}$=1上的一点P与两焦点F1,F2所构成的三角形称为焦点三角形.分析 (1)利用椭圆定义知|PF1|+|PF2|为定值2a,再利用均值定理求积|PF1|•|PF2|的最大值即可;
(2)由椭圆的定义可知||MF1|+|MF2||=2a,|F1F2|=2c,设∠F1MF2=θ,
在△F1AF2中,由余弦定理可得:|F1F2|2=|MF1|2+|MF2|2-2|MF1|•|MF2|cosθ=(|MF1|+|MF2|)2-2|MF1|•|MF2|(1+cosθ),
可得4c2=4a2-2|MF1|•|MF2|(1+cosθ)⇒|MF1|•|MF2|=$\frac{2{b}^{2}}{1+cosθ}$
即有△F1MF2的面积S=|MF1|•|MF2|sin∠F1MF2=${b}^{2}\frac{sinθ}{1+cosθ}={b}^{2}tan\frac{θ}{2}=tan\frac{θ}{2}$.
解答 解:(1),设P(x,y),∴F1(-$\sqrt{3}$,0),F2(-$\sqrt{3}$,0),
则$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=(-$\sqrt{3}$-x,-y)•($\sqrt{3}$-x,-y)=x2+y2-3=$\frac{3}{4}$x2-2
∵x2∈[0,4],∴=$\frac{3}{4}$x2-2∈[-2,1].
∴$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最大值为1,最小值为-2.
证明:(2)由椭圆的定义可知||MF1|+|MF2||=2a,|F1F2|=2c,设∠F1MF2=θ,
在△F1AF2中,由余弦定理可得:
|F1F2|2=|MF1|2+|MF2|2-2|MF1|•|MF2|cosθ=(|MF1|+|MF2|)2-2|MF1|•|MF2|(1+cosθ),
可得4c2=4a2-2|MF1|•|MF2|(1+cosθ)⇒|MF1|•|MF2|=$\frac{2{b}^{2}}{1+cosθ}$
即有△F1MF2的面积S=|MF1|•|MF2|sin∠F1MF2=${b}^{2}\frac{sinθ}{1+cosθ}={b}^{2}tan\frac{θ}{2}=tan\frac{θ}{2}$.
点评 本题考查椭圆方程的求法,考查$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最大值与最小值的求法,焦点三角形的面积,解题时要认真审题,注意椭圆性质的合理运用.属于中档题


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既非充分也非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{\sqrt{3}}{3}$) | B. | (-∞,$\frac{\sqrt{3}}{3}$] | C. | (-∞,-$\frac{\sqrt{3}}{3}$) | D. | (-∞,-$\frac{\sqrt{3}}{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com