Question

2．观察下列砌钢管的横截面图：

则第n个图的钢管数是$\frac{3}{2}{n^2}+\frac{3}{2}n$．（用含n的式子表示）

Answer 1

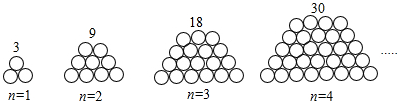
分析 本题可依次解出n=1，2，3，…，钢管的个数．再根据规律以此类推，可得出第n堆的钢管个数．

解答 解：第一个图中钢管数为1+2=3；
第二个图中钢管数为2+3+4=9；
第三个图中钢管数为3+4+5+6=18；
第四个图中钢管数为4+5+6+7+8=30，
依此类推，第n个图中钢管数为n+（n+1）+（n+2）+…+2n=$（2n+n）×\frac{n}{2}+\frac{2n+n}{2}$=$\frac{3}{2}{n^2}+\frac{3}{2}n$，
故答案为：$\frac{3}{2}{n^2}+\frac{3}{2}n$．

点评 本题考查归纳推理．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．