
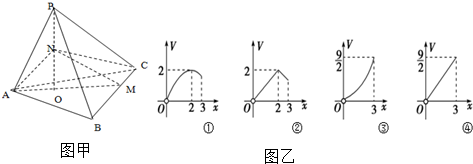
分析 由题意直接求出三棱锥N-AMC的体积V与x变化关系,通过函数表达式,确定函数的图象即可.
解答 :底面三角形ABC的边AC=3,CM=x,∠ACB=30°,
∴△ACM的面积为:$\frac{1}{2}$x•3•sin30°=$\frac{3}{4}$x,
又∵三棱锥N-AMC的高NO=PO-PN=8-2x
所以三棱锥N-AMC的体积V=$\frac{1}{3}$(8-2x)•$\frac{3}{4}$x=-$\frac{1}{2}$x2+2x
当x=2时取得最大值,开口向下的二次函数,
故答案为:①
点评 本题考查几何体的体积与函数之间的关系,求出底面三角形的面积,是本题的一个关键步骤,通过二次函数研究几何体的体积的变化趋势是本题的特点,是好题,新颖题目,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
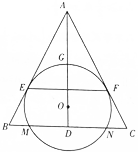 如图,O为等腰三角形ABC内一点,圆O与△ABC的底边BC交于M、N两点与底边上的高AD交于点G,与AB、AC分别相切于E、F两点.
如图,O为等腰三角形ABC内一点,圆O与△ABC的底边BC交于M、N两点与底边上的高AD交于点G,与AB、AC分别相切于E、F两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在(-∞,-1)上单调递增 | |
| B. | 函数f(x)在(-∞,-1)上单调递减 | |
| C. | 若b=0,则函数f(x)的图象与直线y=10只有一个公共点 | |
| D. | 若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com