
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
分析 设M(x1,y1),N(x2,y2),线段MN中点P(x0,y0),利用点差法能求出$\frac{m}{n}$的值.
解答 解:设M(x1,y1),N(x2,y2),线段MN中点P(x0,y0).
由$\left\{\begin{array}{l}{m{{x}_{1}}^{2}+n{{y}_{1}}^{2}=1}\\{m{{x}_{2}}^{2}+n{{y}_{2}}^{2}=1}\end{array}\right.$,两式相减得m(${{x}_{1}}^{2}-{{x}_{2}}^{2}$)+n(${{y}_{1}}^{2}-{{y}_{2}}^{2}$)=0.
又x1+x2=2x0,y1+y2=2y0,
∵直线y=1-4x,∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-4,
∴mx0-4ny0=0,
∵kOP=$\frac{{y}_{0}}{{x}_{0}}$=$\frac{\sqrt{2}}{2}$.
∴$\frac{m}{n}$=$\frac{4{y}_{0}}{{x}_{0}}$=2$\sqrt{2}$.
故选:C.
点评 本题考查实数值比值的求法,是中档题,解题时要认真审题,注意点差法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | ¬p∧¬q | B. | ¬p∧q | C. | p∧¬q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
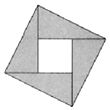 如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.
如图,阴影部分是由四个全等的直角三角形组成的图形,若直角三角形两条直角边的长分别为a,b,且a=2b,则在大正方形内随即掷一点,这一点落在正方形内的概率为$\frac{1}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com