考点:与二面角有关的立体几何综合题,平面与平面平行的判定
专题:证明题,空间位置关系与距离,空间角
分析:(Ⅰ)连接BD,由已知条件推导出BD⊥平面AA
1C
1C,由此能证明BD⊥AA
1.
(Ⅱ)由已知条件推导出AB
1∥平面DA
1C
1,B
1C∥平面DA
1C
1,由此能够证明平面AB
1C∥平面DA
1C
1.
(Ⅲ)设AC交BD于O,连接A
1O,以O为坐标原点建立空间直角坐标系,设OB=1利用向量法能求出P为CC
1的中点时,平面PDA
1和平面DA
1C
1所成的锐二面角的余弦值为
.
解答:
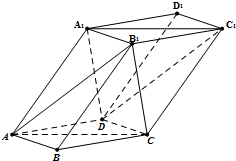
(Ⅰ)证明:连接BD,∵平面ABCD为菱形,∴BD⊥AC,
∵平面AA
1C
1C⊥平面ABCD,且交线为AC,
∴BD⊥平面AA
1C
1C,
又∵A
1A?平面AA
1C
1C,
∴BD⊥AA
1.…(4分)
(Ⅱ)证明:由棱柱的性质知B
1C
1∥AD,且B
1C
1=AD
∴四边形AB
1C
1D为平行四边形,
∴AB
1∥DC
1,∵AB
1在平面DA
1C
1外,DC
1?平面DA
1C
1∴AB
1∥平面DA
1C
1,…(5分)
同理B
1C∥平面DA
1C
1,…(6分)
∵AB
1∩B
1C=B
1,∴平面AB
1C∥平面DA
1C
1.…(7分)
(Ⅲ)解:设AC交BD于O,连接A
1O,
∵菱形AA
1C
1C,且∠A
1AC=60°,
∴△A
1AC是等边三角形,且O为AC中点,∴A
1O⊥AC,
又∵平面AA
1C
1C⊥平面ABCD,平面AA
1C
1C∩平面ABCD=AC,
∴A
1O⊥平面ABCD,又BD⊥AC,
如图,以O为坐标原点建立空间直角坐标系,设OB=1,…(8分)
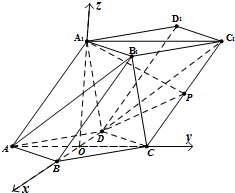
则
OA=,
AA1=2,A1O=3,
∴B(1,0,0),D(-1,0,0),A(0,-
,0),
C(0,
,0),A
1(0,0,3),
∴
==(0,2,0),
=(1,0,3),
=(0,,3),
设
=λ=(0,λ,3λ),
则
=+=(1,λ+,3λ),
设平面DA
1C
1和平面PDA
1的法向量分别为:
=(x1,y1,z1),=(x2,y2,z2),
∵
•=2y1=0,•=x1+3z1=0,
∴
=(-3,0,1),
| | •=x2+3z2=0, | | •=x2+(λ+)y2+3λz2=0 |
| |
∴
=(-3,,1),…(10分)
∵|cos<
,
>|=|
|=
,
∴2λ
2-5λ+2=0,解得
λ=或λ=2(舍去),…(11分)
当P为CC
1的中点时,平面PDA
1和平面DA
1C
1所成的锐二面角的余弦值为
.…(12分)
点评:本题考查异面直线垂直的证明,考查平面与平面平行的证明,考查满足条件的点的位置的求法,解题时要认真审题,注意空间思维能力的培养.

 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形且∠A1AC=∠DAB=60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,四边形AA1C1C也为菱形且∠A1AC=∠DAB=60°,平面AA1C1C⊥平面ABCD.



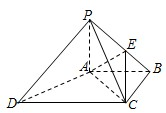 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD.底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC=3,点E在棱PB上,且PE=2EB.
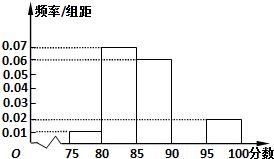 某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格. 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD.