
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100] |
| 频数(个) | 10 | 50 | m | 15 |
分析 (1)根据频率与样本容量的关系,列出方程求出m、n的值,得出众数的值;
(2)根据分层抽样法求出[80,85)和[95,100]中抽取的个数,利用列举法求出基本事件数,计算对应的概率值.
解答 解:(1)依题意可得,$\left\{\begin{array}{l}\frac{m}{n}=\frac{4}{19}\\ n=10+50+15+m\end{array}$,
解得m=20,n=95,(4分)
据表知该样本的众数的近似值是87.5;(5分)
(2)若采用分层抽样的方法从重量在[80,85)和[95,100]的土鸡蛋中共抽取5个,
则重量在[80,85)的个数为$\frac{10}{10+15}$×5=2,记为x,y;(6分)
在[95,100]的个数为$\frac{15}{10+15}$×5=3,记为a,b,c;(7分)
从抽出的5个土鸡蛋中,任取2个共有
(x,a),(x,b),(x,c),(a,b),(a,c),
(b,c),(y,a),(y,b),(y,c),(x,y) 10种情况;(9分)
要|g1-g2|>10,则必须是“重量在[80,85)和[95,100]中各有一个”,
这样的情况共有
(x,a),(x,b),(x,c),(y,a),(y,b),(y,c) 6种;
设事件A 表示“抽出的5个土鸡蛋中,任取2个,重量满足|g1-g2|>10”,
则P(A)=$\frac{6}{10}$=$\frac{3}{5}$;
答:从抽出的5个土鸡蛋中,任取2个,重量满足|g1-g2|>10的概率为$\frac{3}{5}$.(11分)
点评 本题考查了频率与样本容量的关系,也考查了分层抽样以及列举法求基本事件数的概率问题,是中档题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,1) | B. | (-5,1) | C. | ($\frac{1}{2}$,1) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
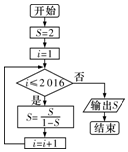
| A. | -$\frac{2}{4029}$ | B. | -$\frac{2}{4030}$ | C. | -$\frac{2}{4031}$ | D. | -$\frac{2}{4033}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com