
分析 (1)利用递推关系即可得出;
(2)法一:直接计算化简即可证明;
法二:利用数学归纳法即可证明.
(3)利用“累加求和”方法、不等式的性质、分类讨论即可得出.
解答 (1)解:当n≥2时,${a_n}={S_n}-{S_{n-1}}=\frac{n(n+1)}{2}-\frac{(n-1)n}{2}=n$,
又∵a1=S1=1,∴an=n.
(2)证明:<法一>:∵$\frac{1}{a_n}=\frac{1}{n}$,∴${T_n}=1+\frac{1}{2}+…+\frac{1}{n}$,
∴${R_{n-1}}=1+(1+\frac{1}{2})+(1+\frac{1}{2}+\frac{1}{3})+…+(1+\frac{1}{2}+…+\frac{1}{n-1})$=$(n-1)•1+(n-2)•\frac{1}{2}+(n-3)•\frac{1}{3}+…+1•\frac{1}{n-1}$
=$n(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n-1}-1+\frac{1}{n})=n(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n-1}+\frac{1}{n}-1)=n({T_n}-1)(n≥2)$.
<法二>:数学归纳法
①n=2时,${R_1}={T_1}=\frac{1}{a_1}=1$,$2({T_2}-1)=2(\frac{1}{{a_1^{\;}}}+\frac{1}{a_2}-1)=1$,
②假设n=k(k≥2,k∈N*)时有Rk-1=k(Tk-1),
当n=k+1时,${R_k}={R_{k-1}}+{T_k}=k(T_k^{\;}-1)+{T_k}=(k+1){T_k}-k=(k+1)({T_{k+1}}-\frac{1}{{{a_{k+1}}}})-k$=$(k+1)({T_{k+1}}-1+1-\frac{1}{k+1})-k=(k+1)({T_{k+1}}-1)$,
∴n=k+1是原式成立
由①②可知当n≥2,n∈N*时Rn-1=n(Tn-1).
(3)解:∵${(1-\frac{m}{n+3})^n}<{(\frac{1}{2})^m}$,m=1,2,…,n.
$\left.{\begin{array}{l}{m=1时,(\frac{n+2}{n+3}{)^n}<\frac{1}{2}}\\{m=2时,(\frac{n+1}{n+3}{)^n}<{{(\frac{1}{2})}^2}}\\{m=3时,(\frac{n}{n+3}{)^n}<{{(\frac{1}{2})}^3}}\\…\\{m=n-1时,(\frac{4}{n+3}{)^n}<{{(\frac{1}{2})}^{n-1}}}\\{m=n时,(\frac{3}{n+3}{)^n}<{{(\frac{1}{2})}^n}}\end{array}}\right\}$⇒相加得,${(\frac{n+2}{n+3})^n}+{(\frac{n+1}{n+3})^n}+…+{(\frac{4}{n+3})^n}+{(\frac{3}{n+3})^n}<\frac{1}{2}+{(\frac{1}{2})^2}+{(\frac{1}{2})^3}+…+{(\frac{1}{2})^{n-1}}+{(\frac{1}{2})^n}$,
∵$\frac{1}{2}+{(\frac{1}{2})^2}+{(\frac{1}{2})^3}+…+{(\frac{1}{2})^{n-1}}+{(\frac{1}{2})^n}=1-{(\frac{1}{2})^n}<1$,
∴3n+4n+…+(n+2)n<(n+3)n,
∴n≥6时,∴3n+4n+…+(n+2)n=(n+3)n无解,
又当n=1时;3<4,n=2时,32+42=52;n=3时,33+43+53=63n=4时,34+44+54+64为偶数,而74为奇数,不符合n=5时,35+45+55+65+75为奇数,而85为偶数,不符合.
综上所述n=2或者n=3.
点评 本题考查了递推关系、学归纳法、“累加求和”方法、不等式的性质、分类讨论方法,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -$\frac{3}{2}$或-2 | D. | $\frac{3}{2}$或-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
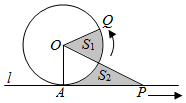 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )| A. | S1=S2 | B. | S1≤S2 | ||
| C. | S1≥S2 | D. | 先S1<S2,再S1=S2,最后S1>S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com